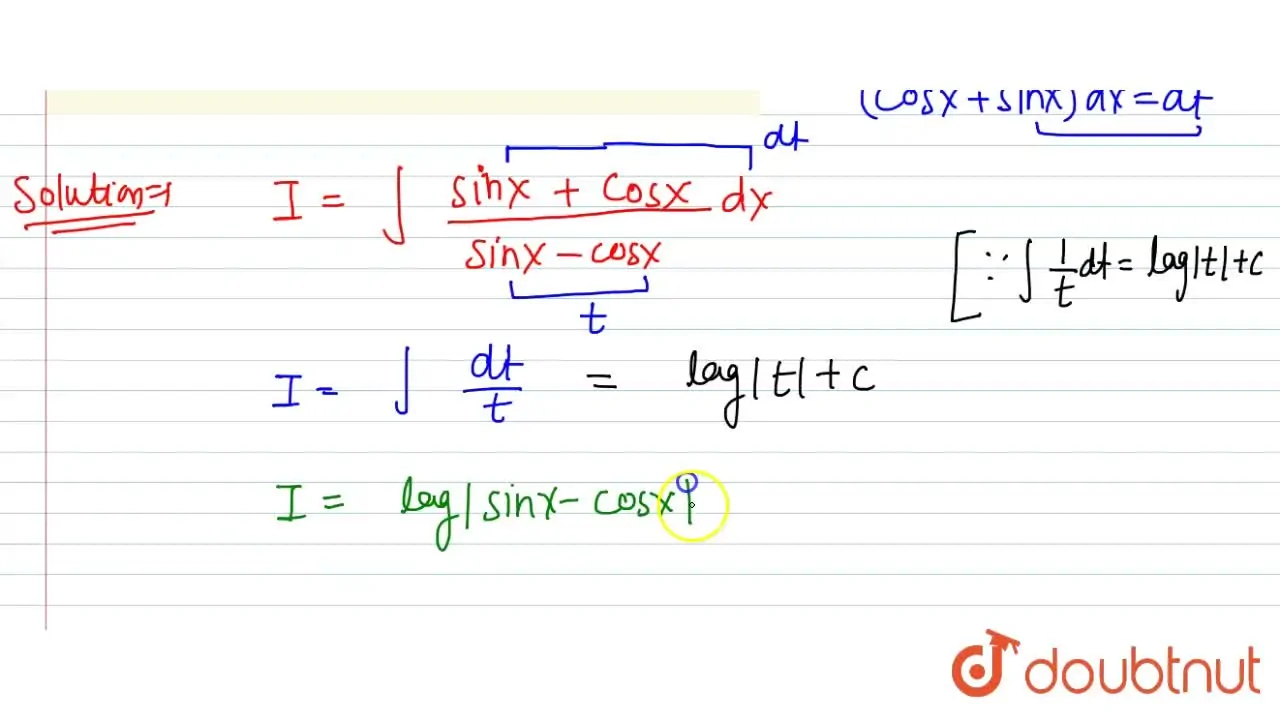
Evaluate: ∫sinx+cosxsinx−cosxdx
Video Solution
|
Answer
Step by step video & image solution for Evaluate: int(sinx+cosx)/(sinx-cosx)dx by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023
Similar Questions
Evaluate: ∫sinx+2cosx2sinx+cosxdx
View SolutionEvaluate: ∫4sinx+5cosx5sinx+4cosx dx
View SolutionEvaluate: ∫2sinx+3cosx3sinx+4cosx dx
View SolutionEvaluate : ∫sinx+cosxsin(x−a)dx
View SolutionEvaluate: ∫sinxsinx−cosxdx
View SolutionEvaluate: ∫(sinx+cosx) dx
View SolutionEvaluate: ∫cosx2+3sinxdx
View SolutionEvaluate: (i) ∫sinx+2cosx2sinx+cosx dx (ii) ∫cos4x−cos2xsin4x−sin2x dx
View SolutionEvaluate ∫sinxcosxdx
View SolutionEvaluate: ∫sinx+cosx9+16sin2x dx
View Solution