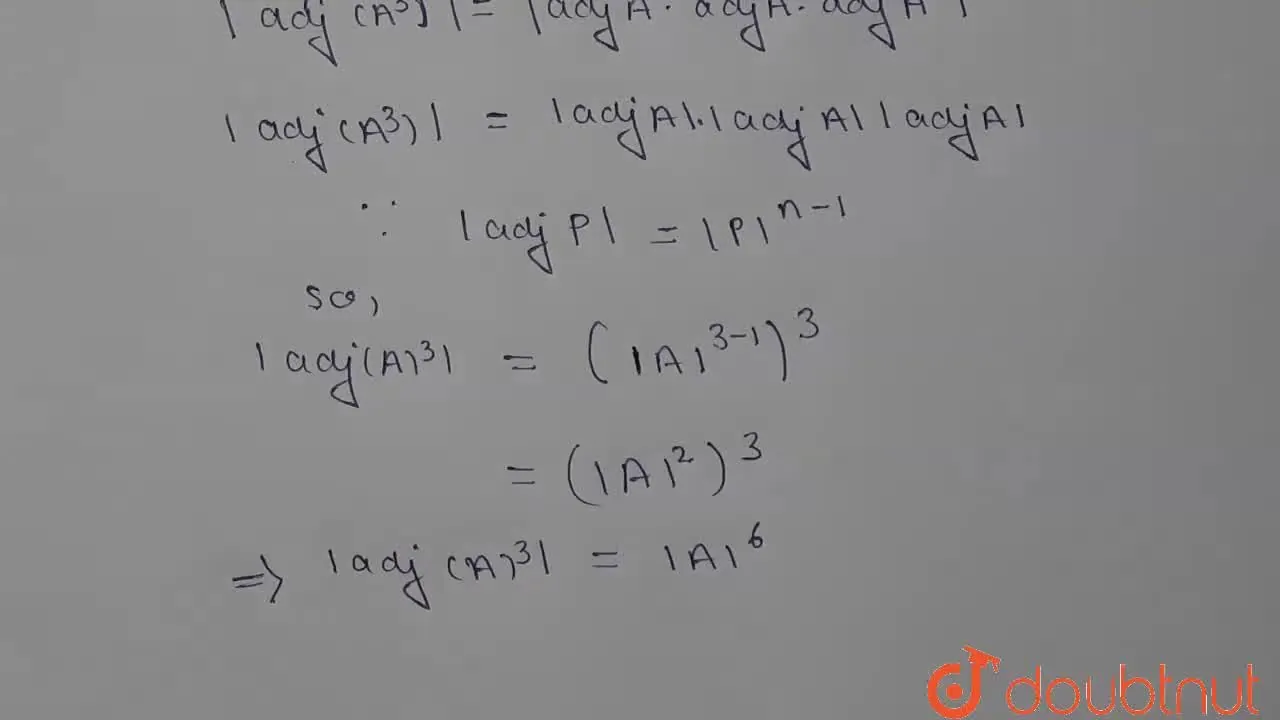If A is a non singular square matrix 3 then ∣∣adj(A3)∣∣ equals (A) |A|8 (B) |A|6 (C) |A|9 (D) |A|12
Step by step video & image solution for If A is a non singular square matrix 3 then |adj(A^3)| equals (A) |A|^8 (B) |A|^6 (C) |A|^9 (D) |A|^12 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
If A is a non singular square matrix then |adj.A| is equal to (A) |A| (B) |A|n−2 (C) |A|n−1 (D) |A|n
View SolutionIf A is a non singular square matrix; then adj(adjA)=|A|n−2A
View SolutionIf A is a non singular square matrix; then adj(adjA)=|A|n−2A
View SolutionIf A is a non singular matrix of order 3 then |adj(adjA)| equals (A) |A|4 (B) |A|6 (C) |A|3 (D) none of these
View SolutionLet A be a non-singular square matrix of order 3 ×3. Then |adj A| is equal to
(A) |A| (B) |A|2(C) |A|3 (D) 3|A|View SolutionIf A is a 2×2 non singular matrix, then adj(adj A) is equal to :
View SolutionIf A is a 2×2 non singular matrix, then adj(adj A) is equal to :
View SolutionLet A a non singular square matrix of order 3×3. Then |adjA| is equal to
View SolutionLet A be a non-singular square matrix of order n. Then; |adjA| =
View SolutionIf A is a non-singular square matrix such that |A|=10 , find ∣∣A−1∣∣
View Solution