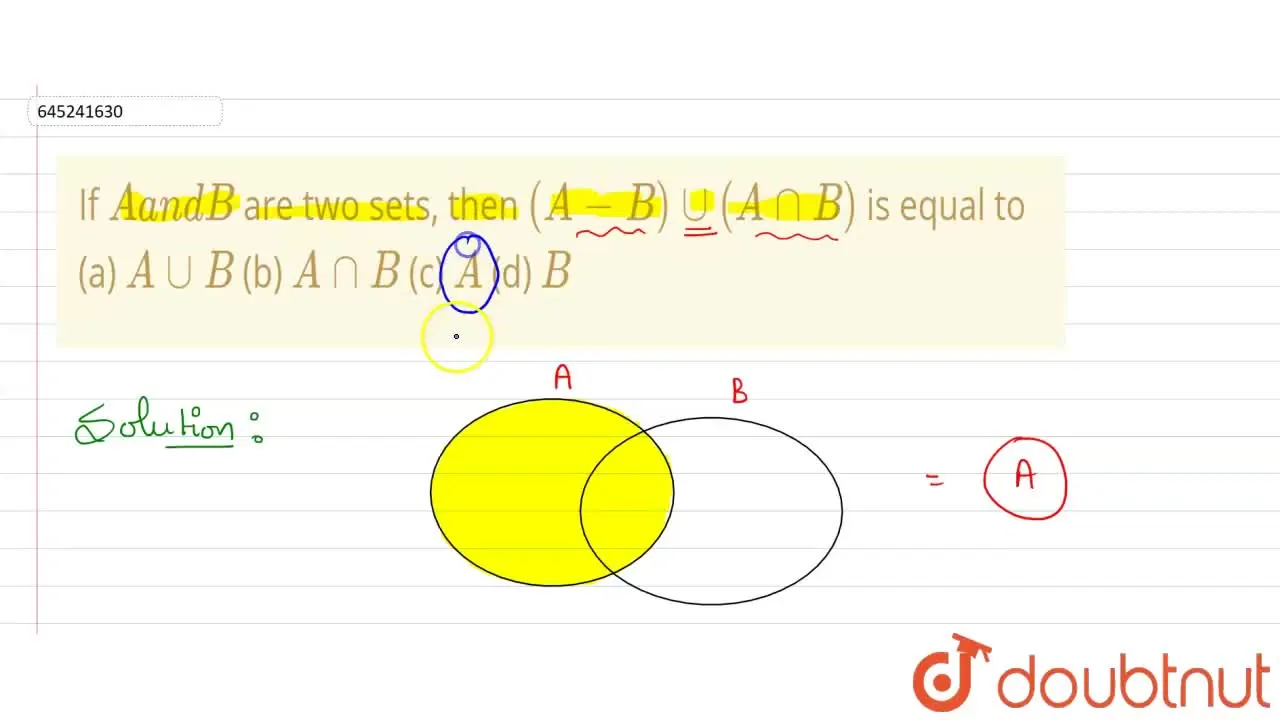
If
are two sets, then
is equal to
(a)
(b)
(c)
(d)
Step by step video & image solution for If Aa n dB are two sets, then (A-B)uu(AnnB) is equal to (a) AuuB (b) AnnB (c) A (d) B by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
Similar Questions
If A and B are two sets ,then (A−B)∪(B−A)∪(A∩B) equals
View SolutionIf A and B are two given sets, then A∩(A∩B)∘ is equal to :
View SolutionIf A and B are two sets, then A∩(A∪B) equals
View SolutionIf A and B are two sets, then A∩(A∪B) equals
View SolutionIf A and B are two sets, then A∩(A∪B)' is equal to - A (b) B (c) ϕ (d) A ∩ B
View SolutionProve that (A∪B)−(A∩B) is equal to (A−B)∪(B−A).
View SolutionIf A and B are two sets then prove that (A∪B)'∪(A'∩B)=A'
View SolutionThe set (A∪B')'∪(B∩C) is equal to
View SolutionFor two sets A and B; A∪B is equal to:
View SolutionFor an two sets A and B,A∩(A∪B) is equal to
(i) A
(ii) B
(iii) ϕ
(iv) A∩BView Solution