A, B, C are three point on a circle. The tangent at A meets BC produced at T,∠BTA=40∘,∠CAT=44∘ . The angle subtended by BC at the centre of the circle is -
84∘
92∘
96∘
104∘
Step by step video & image solution for A, B, C are three point on a circle. The tangent at A meets BC produced at T,angleBTA=40^(@),angleCAT=44^(@) . The angle subtended by BC at the centre of the circle is - by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A, B and C are three points on a circle. The tangent at C meets BA extended at T. Given, ∠ATC=36∘and∠ACT=48∘, the angle subtended by AB at the centre of the circle is
A84∘B48∘C96∘D72∘ - Question 2 - Select One
A, B and C are the three points on a circle such that ∠ABC=35∘and∠BAC=85∘. What is the angle (in degrees) subtended by arc AB at the centre of the circle?
A60B90C135D120 - Question 3 - Select One
A, B and C are three points on a circle with centre O. The tangent at C meets BA produced to T. If ∠ATC=30∘ and ∠ACT=48∘, then what is the value of ∠AOB?
A78∘B96∘C102∘D108∘
The total plane angle subtended by a circle at its centre is
View SolutionIn figure , BOA is a diameter of circle and the tangent at point P meets BA produced at. T if ∠PBO=30∘ then ∠PTA=
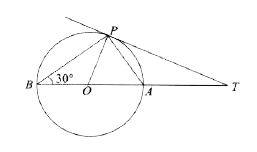 View Solution
View SolutionAB is a diameter of a circle with centre O. The tangents at C meets AB produced at Q. if ∠CAB=34∘, then measure of is ∠CBA is
View SolutionThe angle subtended by the diameter at any point on the circles is a/an_______angle.
View SolutionAB is the diameter of a circle with centre O. The tangent at a point C on the circle meets AB produced at Q. If ∠CAB=42∘, then what is the measure of ∠CQA?
AB एक वृत्त का व्यास है जिसका केंद्र O है | वत्त पर स्थित एक बिंदु C से गुजरने वाली स्पर्श रेखा AB से Q पर मिलती है | यदि ∠CAB=42∘ है, तो ∠CQA का मान क्या होगा ?View Solution
