A mass M splits into two parts m and (M - m) , which are then separated by a certain distance. Wha ratio (m/M) maximize the gravitational force between the path ?
23
34
12
13
The correct Answer is:C
To solve the problem of maximizing the gravitational force between two parts of a mass M that splits into two parts m and (M−m), we can follow these steps:
1. Understanding the Gravitational Force:
The gravitational force F between two masses m and (M−m) separated by a distance r is given by Newton's law of gravitation:
F=G⋅m⋅(M−m)r2
where G is the gravitational constant.
2. Rearranging the Force Equation:
We can express the force in a more convenient form:
F=Gr2⋅m⋅(M−m)
3. Differentiating the Force with Respect to m:
To find the value of m that maximizes the force, we differentiate F with respect to m:
dFdm=Gr2⋅(M−2m)
4. Setting the Derivative to Zero:
To find the maximum, we set the derivative equal to zero:
M−2m=0
Solving for m:
2m=M⟹m=M2
5. Finding the Ratio mM:
Now, we can find the ratio of m to M:
mM=M2M=12
Conclusion:
The ratio mM that maximizes the gravitational force between the two parts is 12.
The gravitational force F between two masses m and (M−m) separated by a distance r is given by Newton's law of gravitation:
F=G⋅m⋅(M−m)r2
where G is the gravitational constant.
We can express the force in a more convenient form:
F=Gr2⋅m⋅(M−m)
To find the value of m that maximizes the force, we differentiate F with respect to m:
dFdm=Gr2⋅(M−2m)
To find the maximum, we set the derivative equal to zero:
M−2m=0
Solving for m:
2m=M⟹m=M2
Now, we can find the ratio of m to M:
mM=M2M=12
The ratio mM that maximizes the gravitational force between the two parts is 12.
Topper's Solved these Questions
- GRAVITATIONBOOK - PHYSICS WALLAHCHAPTER - GRAVITATIONEXERCISE - NEET Past 5 Years Questions
13 Videos
- GRAVITATIONBOOK - PHYSICS WALLAHCHAPTER - GRAVITATIONEXERCISE - NEET Past 5 Years Questions
13 Videos
- GENERAL PRINCIPLES AND PROCESSES OF ISOLATION OF ELEMENTSBOOK - PHYSICS WALLAHCHAPTER - GENERAL PRINCIPLES AND PROCESSES OF ISOLATION OF ELEMENTSEXERCISE - NEET Past 5 Years Questions
14 Videos
- KINETIC THEORY BOOK - PHYSICS WALLAHCHAPTER - KINETIC THEORY EXERCISE - NEET PAST 5 YEARS QUESTIONS
11 Videos
Similar Questions
Mass M is split into two parts m and (M−m), which are then separated by a certain distance. What is the ratio of (m/M) which maximises the gravitational force between the parts ?
View SolutionA mass M is split into two parts m and (M-m) which are then separated by certain distance. Find ratio (m/M) to maximise the gravitational force F=Gm(M−m)r2 between the parts.
Here G = gravitational constant and r is the distance between m and (M-m).
View Solution
Knowledge Check
A mass M splits into two parts m and (M-m), which are separated by a cetain distance. The ratio m/M which maximizes the gravitational force between the parts is
A1:4B1:3C1:2D1:1A mass M at rest is broken into two pieces having masses m and (M-m). The two masses are then separated by a distance r. The gravitational force between them will be maximum when the ratio of the masses [m : (M-m) of the two parts is
A1:1B1:2C1:3D1:4Two spheres of masses (m) and (M - m) are prepared from a sphere of mass M. They are kept at a distance x. For what ratio of mM will the gravitational attraction between them be maximum ?
A14B13C12D34
Mass M is divided into two parts m1, and m2, For a given separation the ratio of m1M for which the gravitational attraction between the two parts becomes maximum is
View SolutionA mass M is broken into two parts of masses m1 and m2. How are m1 and m2 related so that force of gravitational attraction between the two parts is maximum?
View SolutionA body of mass (2M) splits into four masses {m,M−m,m,M−m}, which are rearranged to form a square as shown in the figure. The ratio of Mm for which, the gravitational potential energy of the system becomes maximum is x : 1 . The value of x is ________.
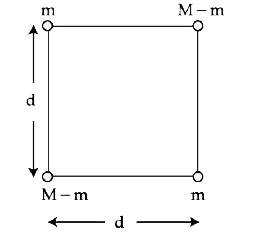
View SolutionThe gravitational force between two particles of masses m1 and m2 separeted by the same distance, then the gravitational force between them will be
View SolutionAssertion : The centres of two cubes of masses m1andm2 are separated by a distance r. The gravitational force between these two cubes will be Gm1m2r2
Reason : According to Newton's law of gravitation, gravitational force between two point masses m1andm2 separated by a distance r is Gm1m2r2.
View Solution