A truck of mass 10 metric ton runs at 3ms−1 along a level track and collides with a loaded truck of mass 20 metric ton, standing at rest. If the trucks couple together , the common speed after the collision is
1ms−1
0.1ms−1
0.5ms−1
0.3ms−1
The correct Answer is:A
To solve the problem step by step, we will use the principle of conservation of momentum. Here's the detailed solution:
Step 1: Identify the masses and velocities before the collision
- Mass of the first truck (m1) = 10 metric tons = 10,000 kg (since 1 metric ton = 1,000 kg)
- Velocity of the first truck (u1) = 3 m/s
- Mass of the second truck (m2) = 20 metric tons = 20,000 kg
- Velocity of the second truck (u2) = 0 m/s (since it is at rest)
Step 2: Calculate the initial momentum of the system
The initial momentum (P_initial) of the system can be calculated using the formula:
Pinitial=m1⋅u1+m2⋅u2
Substituting the values:
Pinitial=(10,000kg⋅3m/s)+(20,000kg⋅0m/s)
Pinitial=30,000kg m/s+0
Pinitial=30,000kg m/s
Step 3: Calculate the final momentum of the system
After the collision, both trucks couple together and move with a common velocity (V). The total mass after the collision is:
mtotal=m1+m2=10,000kg+20,000kg=30,000kg
The final momentum (P_final) of the system is given by:
Pfinal=mtotal⋅V
Pfinal=30,000kg⋅V
Step 4: Apply the conservation of momentum
According to the conservation of momentum:
Pinitial=Pfinal
30,000kg m/s=30,000kg⋅V
Step 5: Solve for V
To find the common velocity (V), we can rearrange the equation:
V=30,000kg m/s30,000kg
V=1m/s
Conclusion
The common speed after the collision is 1 m/s.
- Mass of the first truck (m1) = 10 metric tons = 10,000 kg (since 1 metric ton = 1,000 kg)
- Velocity of the first truck (u1) = 3 m/s
- Mass of the second truck (m2) = 20 metric tons = 20,000 kg
- Velocity of the second truck (u2) = 0 m/s (since it is at rest)
The initial momentum (P_initial) of the system can be calculated using the formula:
Pinitial=m1⋅u1+m2⋅u2
Pinitial=(10,000kg⋅3m/s)+(20,000kg⋅0m/s)
Pinitial=30,000kg m/s+0
Pinitial=30,000kg m/s
After the collision, both trucks couple together and move with a common velocity (V). The total mass after the collision is:
mtotal=m1+m2=10,000kg+20,000kg=30,000kg
Pfinal=mtotal⋅V
Pfinal=30,000kg⋅V
According to the conservation of momentum:
Pinitial=Pfinal
30,000kg m/s=30,000kg⋅V
To find the common velocity (V), we can rearrange the equation:
V=30,000kg m/s30,000kg
V=1m/s
The common speed after the collision is 1 m/s.
Similar Questions
A block of mass 1kg moving with a speed of 4ms−1, collides with another block of mass 2kg which is at rest. The lighter block comes to rest after collision. The loss in KE of the system is
View SolutionA particle of mass m with an initial velocity uˆi+2uˆj collides with a particle of mass 3m at rest. After collision, the two particles stick together and the combined particle moves with a velocity vˆi+v'ˆj. Which of the following is incorrect?
View SolutionA body of mass 10 kg moving with speed of 3ms−1 collides with another stationary body of mass 5 kg As a result, the two bodies stick togethre. The KE of composite mass will be
View SolutionA block of mass 5 kg moves from left to right with a velocity of 2ms−1 and collides with another block of mass 3 kg moving along the same line in the opposite direction with velocity 4ms−1.
(i) If the collision is perfectly elastic, determine velocities of both the blocks after their collision.
(ii) If coefficient of restitution is 0.6, determine velocities of both the blocks after their collision.
View SolutionA particle of mass m is moving along the x-axis with speed v when It collides with a particle of mass 2m initially at rest. After the collision, the first particle has come to rest and the second particle has split into two equal-mass pieces that are shown in the figure. Which of the following statements correctly describes the speeds of the two places? (θ>0)
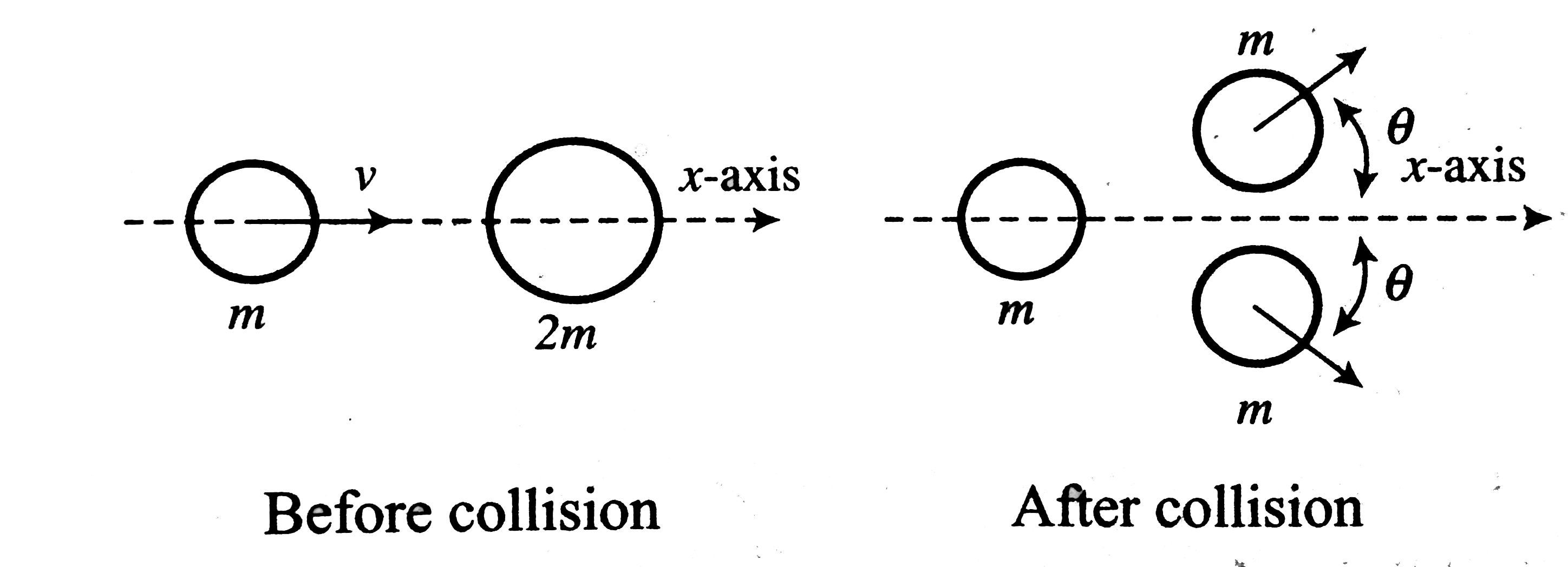
View SolutionA particle A of mass m initially at rest slides down a height of 1.25 m on a frictionless ramp, collides with and sticks to an identical particles B of mass m at rest as shown in the figure.

Then, particles A and B together collide elastically with particle G of mass 2m at rest. The speed of particle G after the collision with combined body (A+B) would be (Take, g=10ms−2)
View SolutionOn a friction surface a block a mass M moving at speed v collides elastic with another block of same mass M which is initially at rest . After collision the first block moves at an angle θ to its initial direction and has a speed v3. The second block's speed after the collision is
View SolutionParticle A of mass mA=m2 moving along the x - axis with velocity v0 collides elastically with another particle B at rest having mass mB=m3 . If both particles move along the x - axis after the collision , the change Δλ in de - Broglie wavelength of particle A , in terms of its de - Broglie wavelength (λ0) before collision is :
View SolutionA neutron of mass 1.67×10−27 kg moving with a speed of 3×106ms−1 collides with a deutron of mass 3.34×10−27 kg which is at rest. After collision, the neutron sticks to the deutron and forms a triton. What is the speed of the triton?
View SolutionParticle A of mass m1 moving with velocity (√3ˆi+ˆj)ms−1 collides with another particle B of mass m2 which is at rest initially. Let →V1and→V2 be the velocities of particles A and B after collision respectively. If m1=2m2 and after collision →V1−(ˆi+√3ˆj)ms−1, the angle between →V1and→V2 is :
View Solution
