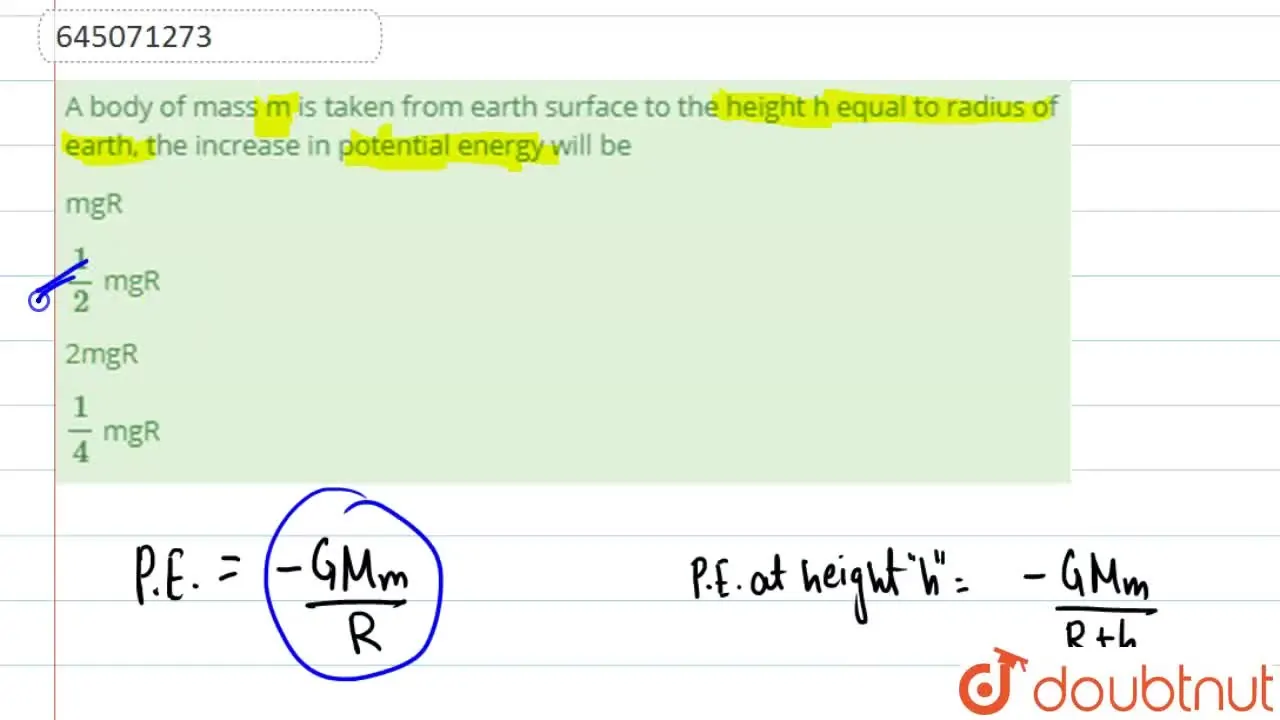
A body of mass m is taken from earth surface to the height h equal to radius of earth, the increase in potential energy will be
mgR
12 mgR
2mgR
14 mgR
The correct Answer is:B
Step by step video & image solution for A body of mass m is taken from earth surface to the height h equal to radius of earth, the increase in potential energy will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
A body of mass 'm' is taken from the earth's surface to the height equal to twice the radius (R) of the earth. The change in potential energy of body will be -
View SolutionA body of mass m taken form the earth's surface to the height is equal to twice the radius (R) of the earth. The change in potential energy of body will be
View SolutionA body of mass m taken form the earth's surface to the height is equal to twice the radius (R) of the earth. The change in potential energy of body will be
View SolutionA body of mass m is thrown from a he equal to radius of earth (A) from earth's surface. The change in potential energy when it reaches to a height equal to 2R from earth's surface is
View SolutionA body of mass m is lifted up from the surface of earth to a height three times the radius of the earth R. The change in potential energy of the body is
View SolutionAn object of mass m is raised from the surface of the earth to a height equal to the radius of the earth, that is, taken from a distance R to 2R from the centre of the earth. What is the gain in its potential energy ?
View SolutionA body of mass m is raised to a height 10 R from the surface of the earth, where R is the radius of the earth. Find the increase in potential energy. (G = universal constant of gravitational, M = mass of the earth and g= acceleration due to gravity)
View SolutionA body of mass m is raised to a height 10 R from the surface of the earth, where R is the radius of the earth. Find the increase in potential energy. (G = universal constant of gravitational, M = mass of the earth and g= acceleration due to gravity)
View SolutionA body of mass m is placed on the earth surface is taken to a height of h=3R, then, change in gravitational potential energy is
View SolutionA body of weight 72 N moves from the surface of earth at a height half of the radius of earth , then geavitational force exerted on it will be
View Solution