For two data sets, each with size 5, the variances are given to be 3 and 4 and the corresponding means are given 2 and 4, respectively. The variance of the combined data set is
112
92
132
52
The correct Answer is:B
To find the variance of the combined data set from two data sets, we can follow these steps:
Step 1: Identify the given values
We have two data sets, each with:
- Size (n1 = n2) = 5
- Variance of the first data set (σ²₁) = 3
- Variance of the second data set (σ²₂) = 4
- Mean of the first data set (x̄₁) = 2
- Mean of the second data set (x̄₂) = 4
Step 2: Calculate the sum of squares for each data set
The formula for variance is given by:
σ2=Σx2in−¯x2
From this, we can rearrange to find the sum of squares:
Σx2i=n⋅σ2+¯x2
For the first data set:
Σx2i=5⋅3+22=15+4=19
For the second data set:
Σy2i=5⋅4+42=20+16=36
Step 3: Calculate the combined mean
The combined mean (M) of both data sets is given by:
M=n1⋅xˉ1+n2⋅xˉ2n1+n2
Substituting the values:
M=5⋅2+5⋅45+5=10+2010=3010=3
Step 4: Calculate the variance of the combined data set
The formula for the variance of the combined data set is:
σ2combined=Σx2i+Σy2in1+n2−M2
Substituting the values we have:
σ2combined=19+3610−32=5510−9=5.5−9=−3.5
This is incorrect; we need to adjust our calculation.
Step 5: Correct calculation for combined variance
The correct formula for combined variance is:
σ2combined=(n1−1)σ21+(n2−1)σ22+n1(xˉ1−M)2+n2(xˉ2−M)2n1+n2−1
Calculating each term:
- (n1−1)σ21=4⋅3=12
- (n2−1)σ22=4⋅4=16
- n1(xˉ1−M)2=5⋅(2−3)2=5⋅1=5
- n2(xˉ2−M)2=5⋅(4−3)2=5⋅1=5
Now substituting into the combined variance formula:
σ2combined=12+16+5+510−1=389≈4.22
Final Answer
The combined variance of the two data sets is approximately 389.
We have two data sets, each with:
- Size (n1 = n2) = 5
- Variance of the first data set (σ²₁) = 3
- Variance of the second data set (σ²₂) = 4
- Mean of the first data set (x̄₁) = 2
- Mean of the second data set (x̄₂) = 4
The formula for variance is given by:
σ2=Σx2in−¯x2
From this, we can rearrange to find the sum of squares:
Σx2i=n⋅σ2+¯x2
Σx2i=5⋅3+22=15+4=19
Σy2i=5⋅4+42=20+16=36
The combined mean (M) of both data sets is given by:
M=n1⋅xˉ1+n2⋅xˉ2n1+n2
Substituting the values:
M=5⋅2+5⋅45+5=10+2010=3010=3
The formula for the variance of the combined data set is:
σ2combined=Σx2i+Σy2in1+n2−M2
Substituting the values we have:
σ2combined=19+3610−32=5510−9=5.5−9=−3.5
This is incorrect; we need to adjust our calculation.
The correct formula for combined variance is:
σ2combined=(n1−1)σ21+(n2−1)σ22+n1(xˉ1−M)2+n2(xˉ2−M)2n1+n2−1
- (n1−1)σ21=4⋅3=12
- (n2−1)σ22=4⋅4=16
- n1(xˉ1−M)2=5⋅(2−3)2=5⋅1=5
- n2(xˉ2−M)2=5⋅(4−3)2=5⋅1=5
σ2combined=12+16+5+510−1=389≈4.22
The combined variance of the two data sets is approximately 389.
Similar Questions
For two data sets, each of size 5, the variances are given to be 4 and 5 and the corresponding means are given to be 2 and 4, respectively. The variance of the combined data set is
(1) 112
(2) 2
(3) 132
(4) 52
View SolutionFor two data sets, each of size 5, the variances are given to be 4 and 5 and the corresponding means are given to be 2 and 4, respectively. The variance of the combined data set is (1) 112 (2) 2 (3) 132 (4) 52
View Solution
Knowledge Check
IF the mean and the variance of a binomial distribution are 4 and 3 respectively , then the probability of six successes is
A.16C6(14)6(34)10B.16C6(14)10(34)6C.12C6(14)6(34)6D.12C6(14)6(34)10
For two data sets each of size 5 the variances are given by 4 and 5 and the corresponding means are given to be 2 and 4 respectively. Then find the variance of the combined data.
View SolutionVariance of the data 2,4,6,8,10 is
View SolutionThe mean of two samples of sizes 200 and 300 were found to be 25, 10 respectively. Their standard deviations were 3 and 4 respectively. The variance of combined sample of size 500 is
View SolutionFor two firms A and B belonging to the same industry the following data is given
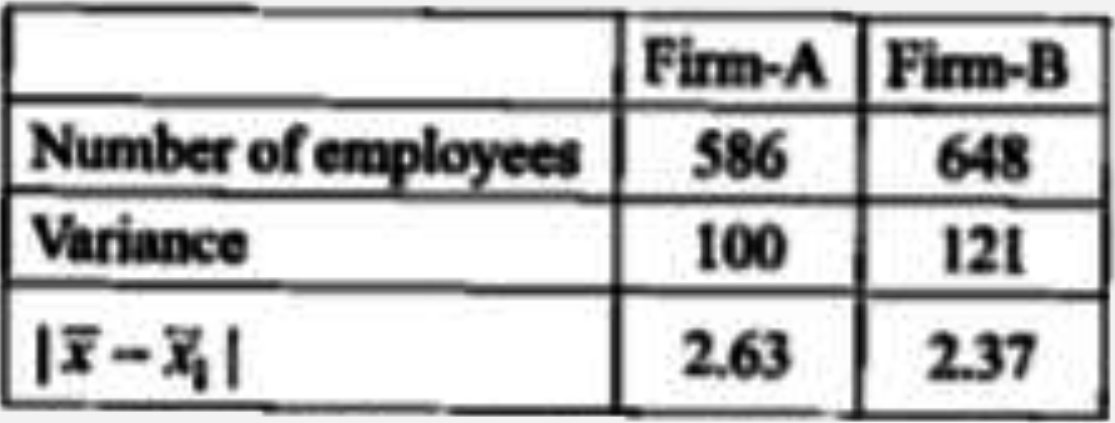
Find the combined variance of the two firms
View SolutionThe mean and the variance of a binomial distribution are 4 and 2 respectively.then, the probabitly of 2 , successes is
View SolutionThe mean and variance of a random variable X having a binomial distribution are 4and2 respectively. The P(X=1) is
View SolutionMean and Variance of a binomial variance are 4 and 4/3 respectively then P(X≥1) will be
View Solution

