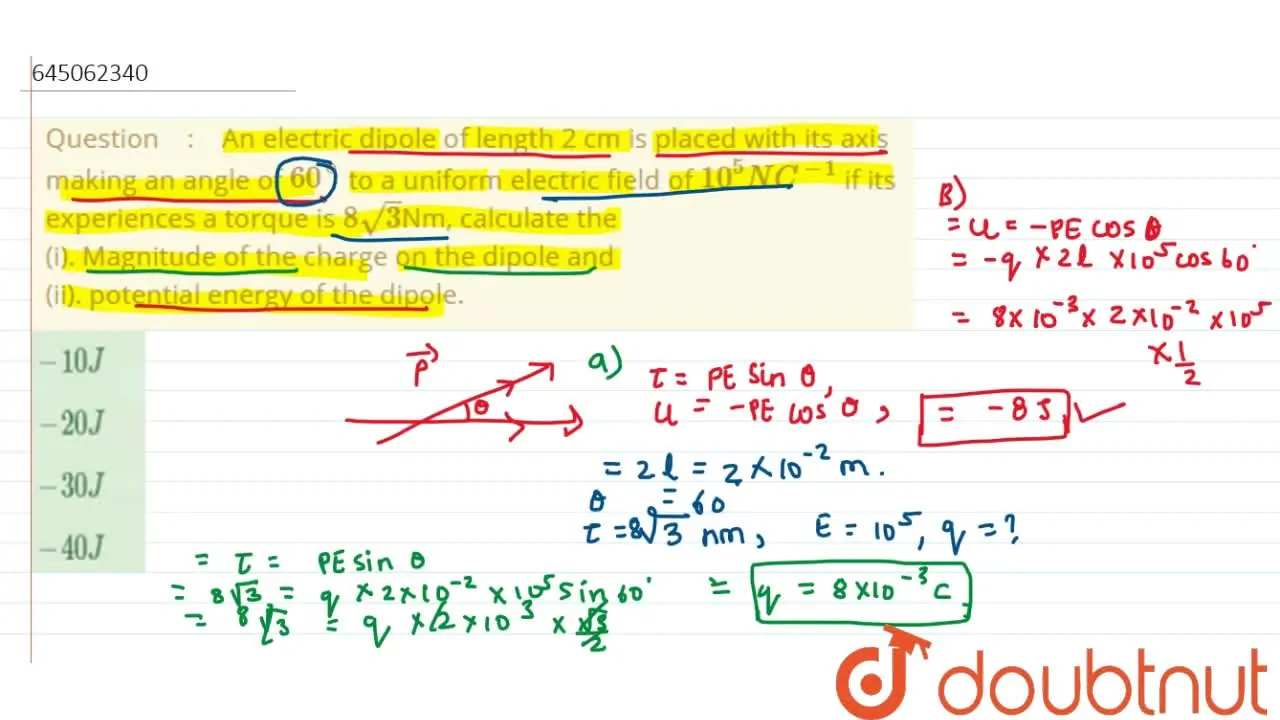
An electric dipole of length 2 cm is placed with its axis making an angle of to a uniform electric field of if its experiences a torque is Nm, calculate the
(i). Magnitude of the charge on the dipole and
(ii). potential energy of the dipole.
The correct Answer is:C
Step by step video & image solution for An electric dipole of length 2 cm is placed with its axis making an angle of 60^(@) to a uniform electric field of 10^(5)NC^(-1) if its experiences a torque is 8sqrt(3)Nm, calculate the (i). Magnitude of the charge on the dipole and (ii). potential energy of the dipole. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
An electric dipole of length 2cm is placed with its axis making an angle 30∘ to a uniform electric field 105NC .If it experiences a torque of 10√3Nm ,then potential energy of the dipole ..
View SolutionAn electric dipole of length 4 cm, when placed with its axis making an angle of 60∘ with a uniform electric field, experiences a torque of 4√3Nm. Calculate the
a. magnitude of the electric field, and
b. potential energy of the dipole, if the dipole has charges of ±8nC.View SolutionAn electric dipole of length 1cm, which places with its axis making an angle of 60∘ with uniform electric field, experience a torque ot 6√3Nm, Calculate potential energy.
View SolutionAn electric dipole is placed at an angle 60∘ with an electric field of strength 4×105 N/C. It experiences a torque equal to 8√3 Nm. Calculate the charge on the dipole, if dipole is of length 4 cm
View SolutionAn electric dipole placed at an angle of 30∘ with a uniform electric field of intensity 104N.C−1 experiences a torque of 9×10−26N.m. What is the moment of the electric dipole?
View SolutionAn electric dipole is placed at an angle of 30∘ to a non-uniform electric field. The dipole will experience
View SolutionAn electric dipole of length 10cm having charges ±6×10−3C, placed at 30∘ with respect to a uniform electric field experiences a torque of magnitude 6√3N−m. Calculate (i) magnitude of electric field (ii) the potential energy of dipole.
View SolutionAn electric dipole is placed at an angle of 30∘ with an electric field intensity 2×105N/C. It experiences a torque equal to 4Nm. The charge on the dipole, if the dipole is length is 2cm, is
View SolutionAn electric dipole is placed at an angle of 30∘ with an electric field intensity 2×105N/C. It experiences a torque equal to 4Nm. The charge on the dipole, if the dipole is length is 2cm, is
View SolutionAn electric dipole, when held at 30∘ with respect to a uniform electric field of 104N/C experiences a torqueof 9×10−26Nm. Calculate dipole moment of the dipole.
View Solution