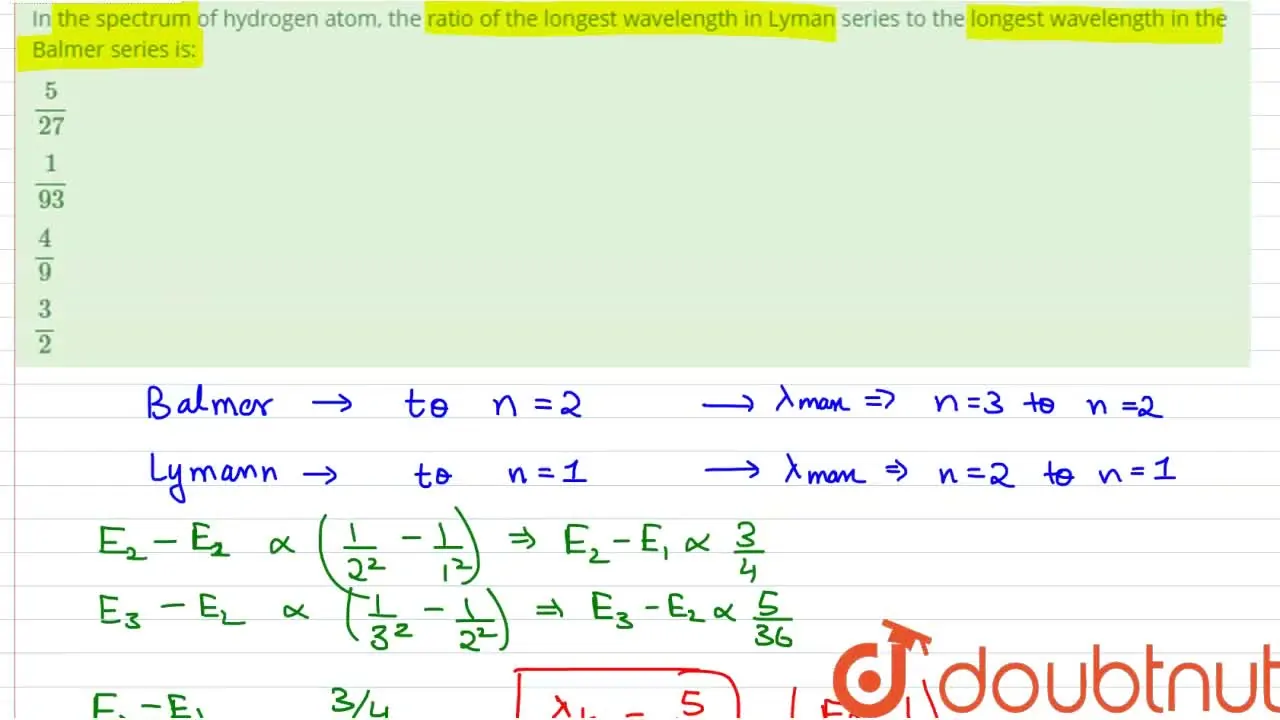
In the spectrum of hydrogen atom, the ratio of the longest wavelength in Lyman series to the longest wavelength in the Balmer series is:
527
193
49
32
The correct Answer is:A
Step by step video, text & image solution for In the spectrum of hydrogen atom, the ratio of the longest wavelength in Lyman series to the longest wavelength in the Balmer series is: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
In the spectrum of hydrogen atom, the ratio of the longest wavelength in Lyman series to the longest wavelangth in the Balmer series is:
View SolutionIn the spectrum of hydrogen atom, the ratio of the longest wavelength in Lyman series to the longest wavelangth in the Balmer series is:
View SolutionIn the spectrum of hydrogen atom, the ratio of the longest wavelength in Lyman series to the longest wavelangth in the Balmer series is
View SolutionIn the spectrum of hydrogen atom, the ratio of the longest wavelength in Lyman series to the longest wavelangth in the Balmer series is:
View SolutionThe shortest wavelength in Lyman series is 91.2 nm. The longest wavelength of the series is
View SolutionIf the shortest wavelength of H atom in Lyman series is x, then longest wavelength in Balmer series of H–atom is
View SolutionThe shortest wavelength of H-atom in Lyman series is x, then longest wavelength in Balmer series of He+ is
View SolutionThe shortest wavelength of H-atom in Lyman series is x, then longest wavelength in Balmer series of He+ is
View SolutionAssertion It is essential that all the lines availabel in the emission spectrum will also be available in the absorption spectrum
Reason The spectrum of hydrogen atom in only absorption spectrum.View SolutionFind the longest wavelength present in the Balmer series of hydrogen.
View Solution