The relation between specles richness and area Is described on a logarithmic scale by the equaton (where 8 - specles richness, A= area, Z = slope of the line (regression co-efficient), C=Y-Intercept].
log S= log C-Z log A
log S= Z log A
log S = log C+ Z log A
log S = log C
The correct Answer is:C
To solve the problem regarding the relationship between species richness (S) and area (A) using the logarithmic scale, we can follow these steps:
1. Understanding the Variables:
- Identify the variables in the equation:
- S = Species richness
- A = Area
- Z = Slope of the line (regression coefficient)
- C = Y-Intercept
2. Establish the Equation:
- The relationship is given by the equation:
logS=logC+Z⋅logA
- This equation indicates that the logarithm of species richness (S) is a linear function of the logarithm of area (A).
3. Graphical Representation:
- On a graph, plot the area (A) on the x-axis and species richness (S) on the y-axis.
- The relationship is expected to be linear, meaning as the area increases, the species richness also increases.
4. Interpreting the Components:
- Y-Intercept (C): This is the value of S when A is 1 (since log(1)=0).
- Slope (Z): This indicates how much S increases for a unit increase in logA. A steeper slope means a greater increase in species richness with area.
5. Conclusion:
- The equation logS=logC+Z⋅logA effectively describes the species-area relationship, showing that larger areas tend to support more species.
- Identify the variables in the equation:
- S = Species richness
- A = Area
- Z = Slope of the line (regression coefficient)
- C = Y-Intercept
- The relationship is given by the equation:
logS=logC+Z⋅logA
- This equation indicates that the logarithm of species richness (S) is a linear function of the logarithm of area (A).
- On a graph, plot the area (A) on the x-axis and species richness (S) on the y-axis.
- The relationship is expected to be linear, meaning as the area increases, the species richness also increases.
- Y-Intercept (C): This is the value of S when A is 1 (since log(1)=0).
- Slope (Z): This indicates how much S increases for a unit increase in logA. A steeper slope means a greater increase in species richness with area.
- The equation logS=logC+Z⋅logA effectively describes the species-area relationship, showing that larger areas tend to support more species.
Similar Questions
Knowledge Check
The relation between specises richness and area is described on a logarithmic scale by the equation [where S = species richness, A = area, Z = slope of the line (regression coefficient ), C= Y - intercept]
Alog S = log CBlog S = Z log AClogS=logC−ZlogADlogS=logC+ZlogAThe relation between species richness and area is correctly depicted by
ALogS=logC−ZlogABLogS=ZlogACLogS=logC+ZlogADLogS=logCThe relation between species richness and area for a wide variety of taxa (angiosperm plants, birds, bats, freshwater fishes) is a
AParabolaBRectangular hyperbolaCEllipseDStraight line

Study the above graph and answer the following questions -
(i) Identify x and y
(ii) The relation between species richness and area can be denoted as generally
(iii) The value of z lies in range of
(iv) On a log scale the relation between species richness and area is
View SolutionIndicate whether the following statements are true or false :
(i) New York in temperate area has 56 species of birds.
(ii) Tropical biomes unlike temperate ones, are more seasonal, relatively less constant and predictable.
(iii) Relationship between species richness (S) and area (A) turned out to be rectangular hyperboia on a logarithmic scale.
(iv) Slope of regression (Z) is 1.15 for frugivorous birds and mammals in tropical forests of different continents.
View SolutionWhich of the statement are in accordance with the observation of geographer Alexander von Humboldt ?
I. Within a region species, richness increases with increasing explored area but within a limit.
II. The relation between species richness and area is a rectangular hyperbole.
III. The richness of species decreases with the increasing explored area.
IV. There is no relation between the explored area and species richness .
View SolutionThe great German naturalist and geographer Alexander von Humboldt observed that within a region species richness increased with increasing explored area, but only up to a limit. In fact, relation between species richness and area for a wide variety of taxa (angiosperm plants, birds, bats, freshwater fi ishes) turns out to be a rectangular hyperbola. Now find out correct equations shown in the graph.
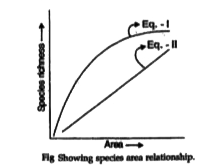
View SolutionIn mollusks of New York state, which of these experiences gives you a value between 0.1 to 0.2?
( S = log of species richness, A = log of Area, C = log of Y- intercept in the species richness area curve)
View Solution

