Let u(t) and v(t) be two solutions of the differential equation $\frac{d y}{d t} = e^{t^{2}} y (t) + sin t with u (2) < v (2)$
Statement 1: $u (t) < v (t)$ for all t
Statement: u-v is proportional ot a positive function of t.

Text Solution

Verified by Experts

The correct Answer is:a

Updated on:21/07/2023

The figure shows the variation of $V$ with $i$ at temperatures $T_{1}$ and $T_{2}$ . Then $T_{1} - T_{2}$ is proportional to

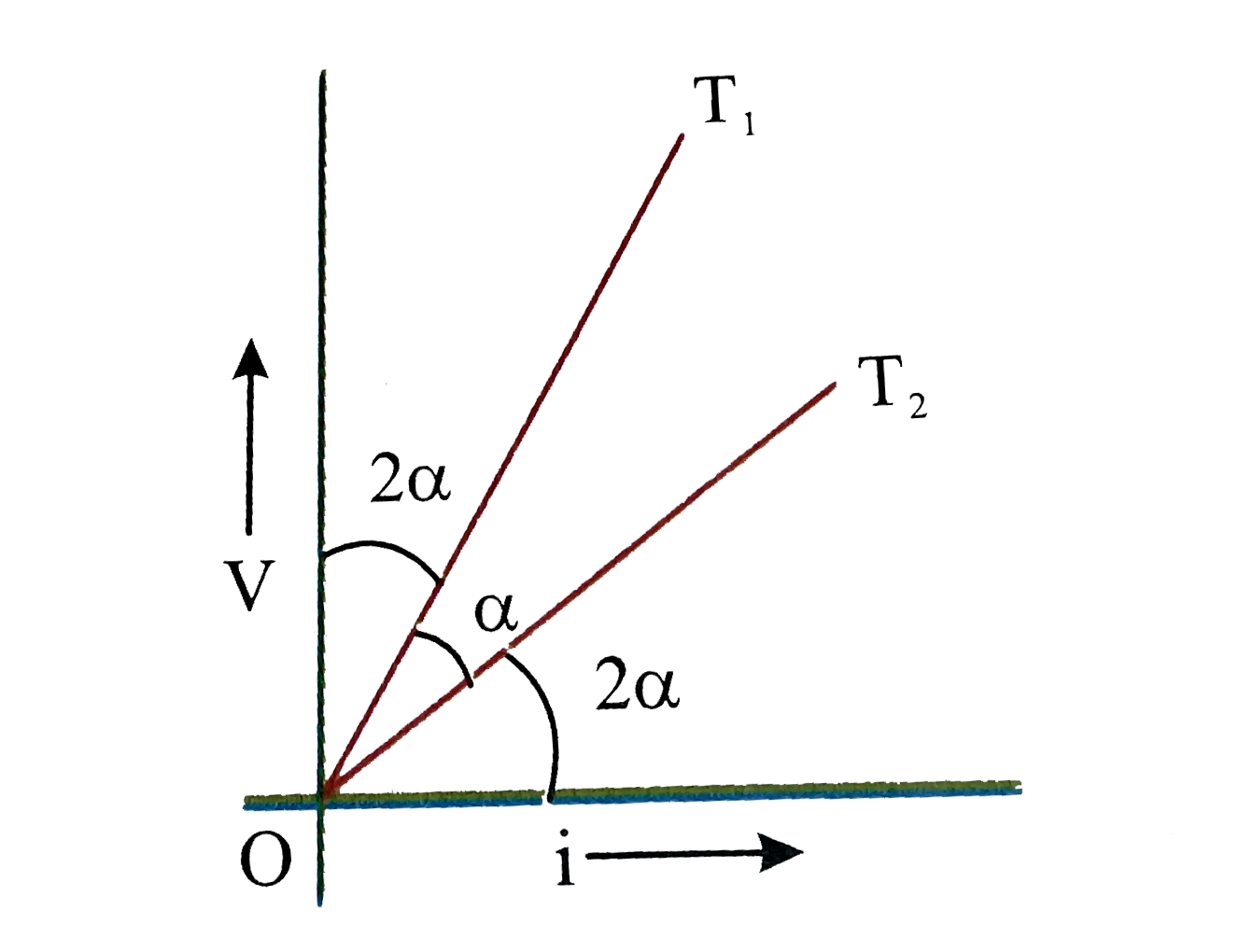A $tan 2 α$
B $tan α$
C $sin α$
D $cos 2 α$
The orthocentre of the triangle formed by the lines $y = 0, (1 + t) x - t y + t (1 + t) = 0$ and $(1 + u) x - u y + u (1 + u) = 0 (t \neq u)$ for all values of t and u lies on the line.
A $x - y = 0$
B $x + y = 0$
C $x - y + 1 = 0$
D $x + y + 1 = 0$