Three resistances, each of 5Ω are connected to form a triangle. Calculate the resistance between two ends of any arm.
Text Solution
According to the question, three 5Ω resistors are connected as shown in the figure.

If we find out the equivalent resistance of between B and C, then R1andR2 are in the series combination.
R.=R1+R2=5+5=10Ω
Now R. and R3 are in the parallel combination.
Hence the equivalent resistance of the circuit is given by
1Req=1R.+1R3⇒1Req=110+15
⇒1Req=310⇒Req=103Ω
|
Updated on:21/07/2023
Knowledge Check
- Question 1 - Select One
Three resistance each of 4Ω are connected to form a triangle. The resistance between any two terminals is
A12ΩB2ΩC6ΩD83Ω - Question 1 - Select One
Three resistances of 2Ω each are connected in a triangle. The resistance in ohms between any two comers is
A3ΩB4ΩC6ΩD43Ω - Question 1 - Select One
Three resistances of 2Ω each are connected in a triangle. The resistance in ohms between any two comers is
A3ΩB4ΩC6ΩD43Ω - Question 1 - Select One
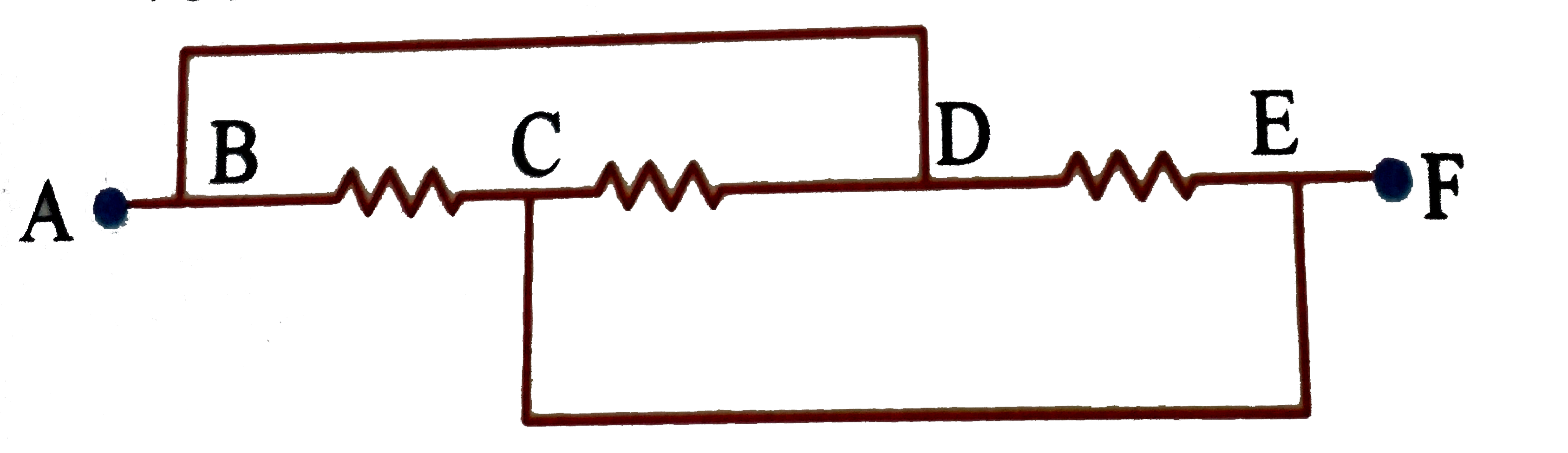
Three resistances each of 3Ω are connected as shown in fig. the resultant resistance between A and F isA9ΩB2ΩC4ΩD1Ω - Question 1 - Select One
Three resistance of 12Ω are connected in the form of an equilateral triangle. The effective resistance between two corners, is
A24ΩB9ΩC12ΩD8Ω - Question 1 - Select One
Three resistors, each of 2Ω are connected together in a triangular shape. The resistance offered between any two vertices will be
A3ΩB6ΩC43ΩD34Ω - Question 1 - Select One
Three resistances 4Ω each of are connected in the form of an equilateral triangle. The effective resistance between two corners is
A8ΩB12ΩC38ΩD83Ω - Question 1 - Select One
Three resistors each of 2 ohm are connected together in a triangular shape. The resistance between any two vertices will be
A4/3 ohmB3/4 ohmC3 ohmD6 ohm

