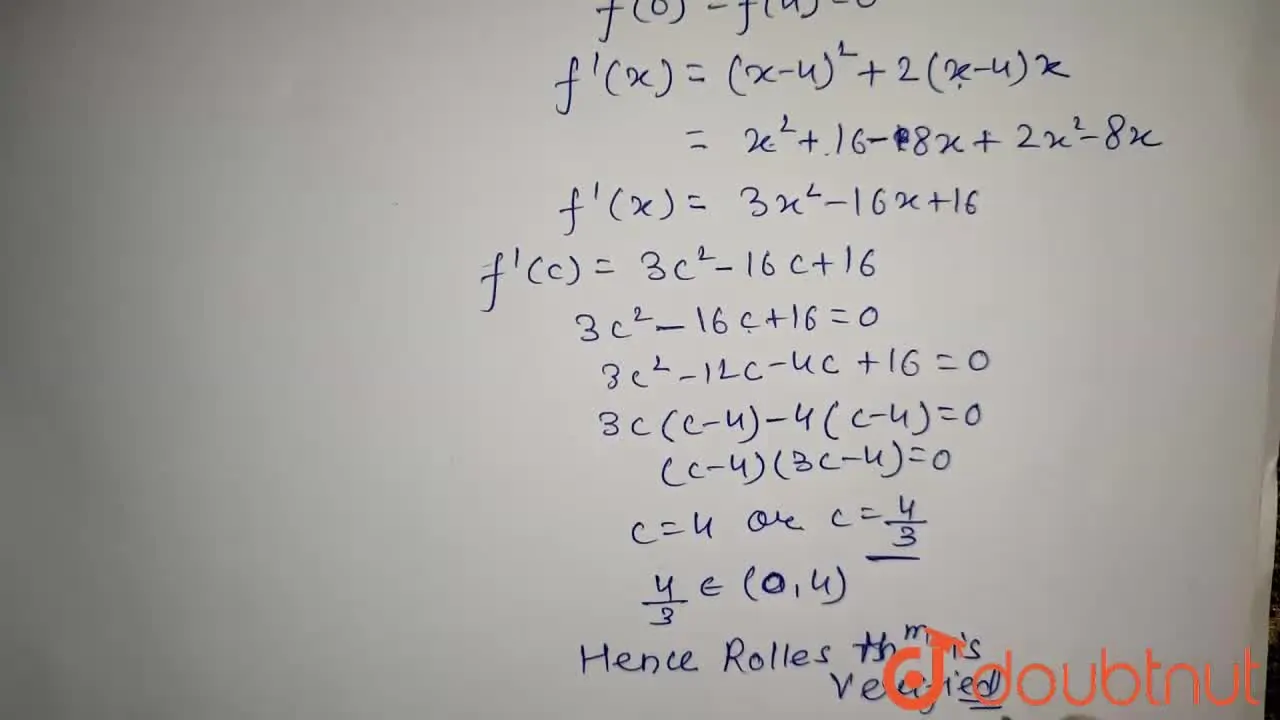Verify Rolle's theorem for the following functions in the given intervals.
f(x) = x(x−4)2 in the interval [0,4].
Step by step video & image solution for Verify Rolle's theorem for the following functions in the given intervals. f(x) = x(x-4)^(2) in the interval [0,4]. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - Continuity and DifferentiabilityEXERCISE - Exercies 5n10videos
Continuity and Differentiability
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - Continuity and DifferentiabilityEXERCISE - Exercies 5o20videos
Continuity and Differentiability
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - Continuity and DifferentiabilityEXERCISE - Exercies 5l18videos
Continuity and Differentiability
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - APPLICATIONS OF INTEGRALSEXERCISE - Miscellaneous Exercise19videos
APPLICATIONS OF INTEGRALS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - DETERMINANTSEXERCISE - Miscellaneous Exercise19videos
DETERMINANTS
Similar Questions
Verify Rolle's theorem for the following functions in the given intervals.
f(x) = x2 in the interval [−2,2].View SolutionVerify Rolle's theorem for the following functions in the given intervals.
f(x) = x2−6x+8 in the interval [2,4].View SolutionVerify Rolle's theorem for the following functions in the given intervals.
(i) f(x) = (x−2)(x−3)2 in the interval [2,3] .
(ii) f(x) = x3(x−1)2 in the interval [0,1].View SolutionVerify Rolle's theorem for the following functions in the given intervals.
f(x)=sin2 x in the interval [0,π].View SolutionVerify Rolle's theorem for the following functions in the given intervals.
f(x) = (x−2)(x−4)(x−6) , in the interval [2,6].View SolutionVerify Rolle's theorem for the following functions in the given intervals.
f(x) = (x−2)4(x−3)3 in the interval [2,3].View SolutionVerify Rolle's theorem for the following functions in the given intervals.
f(x) = x2−5x−6 in the interval [−1,6] .View SolutionVerify Rolle's theorem for the following functions in the given intervals.
f(x) = sin 3x in the interval [0,π].View SolutionVerify Rolle's theorem for the following functions in the given intervals.
f(x) = sinx + cos x in the interval [0,π/2].View SolutionVerify Rolle's theorem for the following functions in the given intervals.
f(x) sin x in the interval [0,π].View Solution