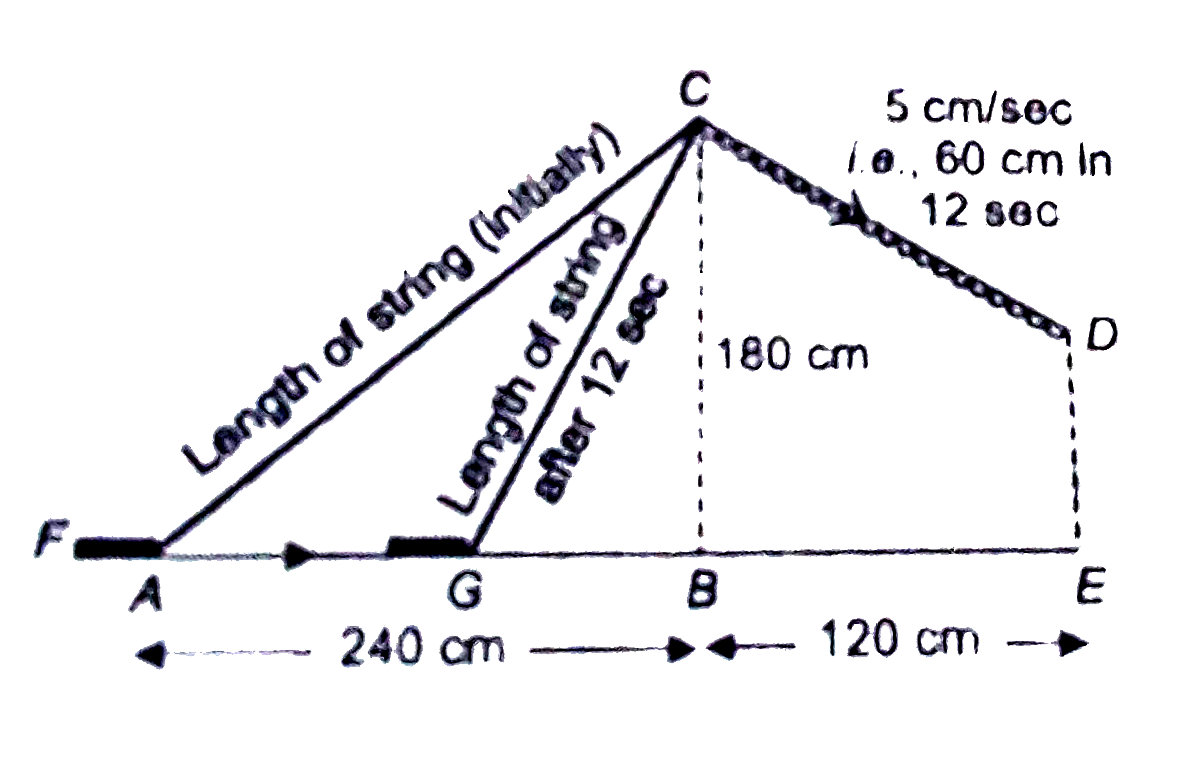
Nazinia is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that h
Description of the figure :
C→ Tip of fishing rod DC
AC→ stiring , AF→ fly
Intially string was AC = √(180)2+(240)2
( by pythagores theorem)
⇒ AC=√32400+57600
= 300 cm
BUT
When Nazima pulls in the string at the rate of 5cm/sec, she will pull 5×12cm in 12 sec. you can imagine that string will pull out 60 cm from C towards D. Now remaining string CA will become CG = 300-60=240 cm , because when string will pull in , its end point A as will as fly will move from A towards G. So, horizontal distance of fly at G ( now) from Nazima at E will be EG.
Now, GB2=CG2−CB2 ( by pythagoras theorem)
=(240)2−(280)2=57600−32400=25200
GB=√25200=10√252=60√7
=60×2.64575=158.745cm
Reqyuired distance = EG = GB + BE= 158.745 + 120
= 278.745 cm = 2.79 m ( approx).
Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar
14 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Exercise 6a
24 Videos
- STATISTICS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
4 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, how much string does she have out? If she pulls in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?

View SolutionIn a pond of water, a flame is held 2 m above the surface of the water. A fish is at depth of 4 m from the water surface. Refractive index of water is 43. The apparent height of the flame from the eyes of fish is -
View SolutionA fish lies at the bottom of a 4m deep water lake. A bird flies 6m above the water surface and refractive index of water is 4/3 . Then the distance between
View SolutionAn aeroplane is flying vertically upwards. When it is at a height of 1000m above the ground and moving at a speed of 367m/s., a shot is fired at it with a speed of 567 ms−1 from a point directly below it. What should be the acceleration of aeroplane so that it may escape from being hit?
View SolutionIn a lake, a fish rising vertically to the surface of water uniformly at the rate of 3 m/s, observes a bird diving vertically towards the water at the rate of 9 m/s. The actual velocity of the dive of the bird is (given, refractive index of water = 4/3)
View SolutionOne end of a light rod of length 1m is attached with a string of length 1m. Other end of the rod is attached at point O such that rod can move in a vertical circle. Other end of the string is attached with a block of mass 2kg. The minimum velocity that must be given to the block in horizontal direction so that it can complete the vertical is (g=10m/s2)
View SolutionA ball of mass 1 kg falls from a height of 5m above the free surface of water. The relative density of the solid ball is s=2/3. The ball travels a distance of 2m under water and becomes stationary. The work done by the resistive forces of water is
View SolutionA rod of length 6m has a mass of 12kg. It is hined at one end of the rod at a distance of 3m below the water surface.
a.What must be the weight of a block that is attached to the other end of the rod so that 5m of the rod's length is under water?
b. Find the magnitude and direction of the force exerted by the hinge on the rod. The specific gravity of the material of rod is 0.5.

View SolutionWater is flowing continuously from a tap of area 10−4m2 the water velocity as it leaves the top is 1m/s find out area of the water stream at a distance 0.15 m below the top
View SolutionWater is flowing condinuously from a tap of area 10−4m2 the water velocity as it leaves the top is 1m/s find out area of the water stream at a distance 0.15 m below the top
View Solution