In Figure, ABC is a right triangle right angled at B and points DandE trisect BC . Prove that 8AE2=3AC2+5AD2.
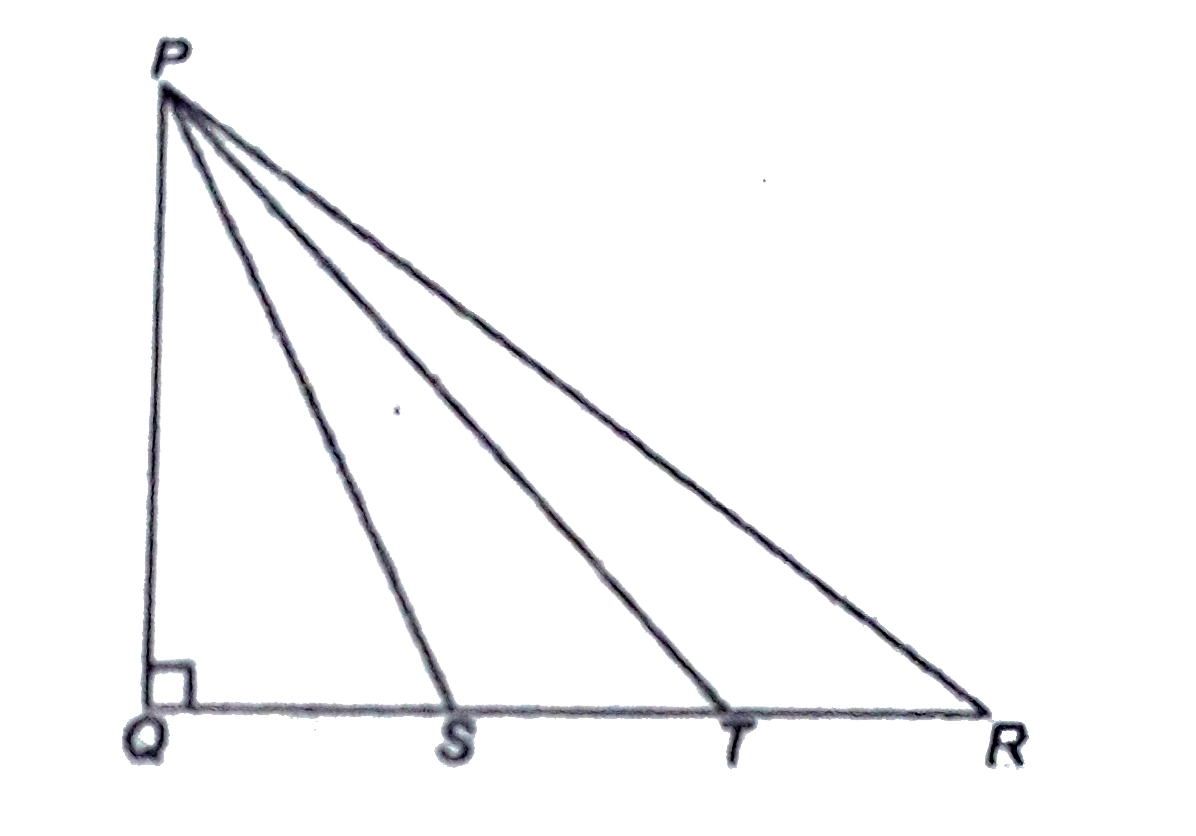
Let QS= ST = TR=x
Now by pythagoras theorem
PR2=PQ2+QR2=PQ2+(3x)2
3PR2=3PQ2+27x2
Also , PS2=PQ2+QS2
(by pythagoras theorem)
=PQ2+x2
⇒ 5PS2=5PQ2+5x2
Adding (1) and (2) ,we get
R.H.S=3PR2+5PS2=8PQ2+32x2=8(PQ2+4x2)=8[PQ2+(2x)2]
=8(PQ2+QT2)=8PT2 ( by Pyhagores theorem)
L.H.S. Hence proved.
Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar
14 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Exercise 6a
24 Videos
- STATISTICS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
4 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
ABC is a right triangle right-angled at B. Let D and E be any points on AB and BC respectively. Prove that AE2+CD2=AC2+DE2
View SolutionABC is a right triangle right-angled at CandAC=√3BC . Prove that ∠ABC=600.
View SolutionA triangle ABC is right angled at A. AL is drawn perpendicular to BC . Prove that ∠BAL=∠ACB.
View SolutionIf ABC is a right triangle right-angled at BandM,N are the mid-points of ABandBC respectively, then 4(AN2+CM2)= (A) 4AC2 (B) 5AC2 (C) 54AC2 (D) 6AC2
View SolutionIn Figure, ABC is a right triangle right angled at B and D is the foot of the the perpendicular drawn from B on AC . If DM⊥BC and DN⊥AB , prove that: (i)DM2=DN×MC (ii)DN2=DM×AN
View SolutionIn Figure, ABC is an obtuse triangle, obtuse angled at B . If AD⊥CB , prove that AC2=AB2+BC2+2 BC×BD .
View SolutionIn the given figure, ΔABC is a right triangle right angled at A. D lies on BA produced and DE⊥BC, intersecting AC at F . if ∠AFE=1300, find
(i) ∠BDE
(ii) ∠BCA
(iii)∠ABC
View SolutionIn figure, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (CYXE)=2ar(△ FCB).
View SolutionIn figure, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: △ FCB≅△ ACE
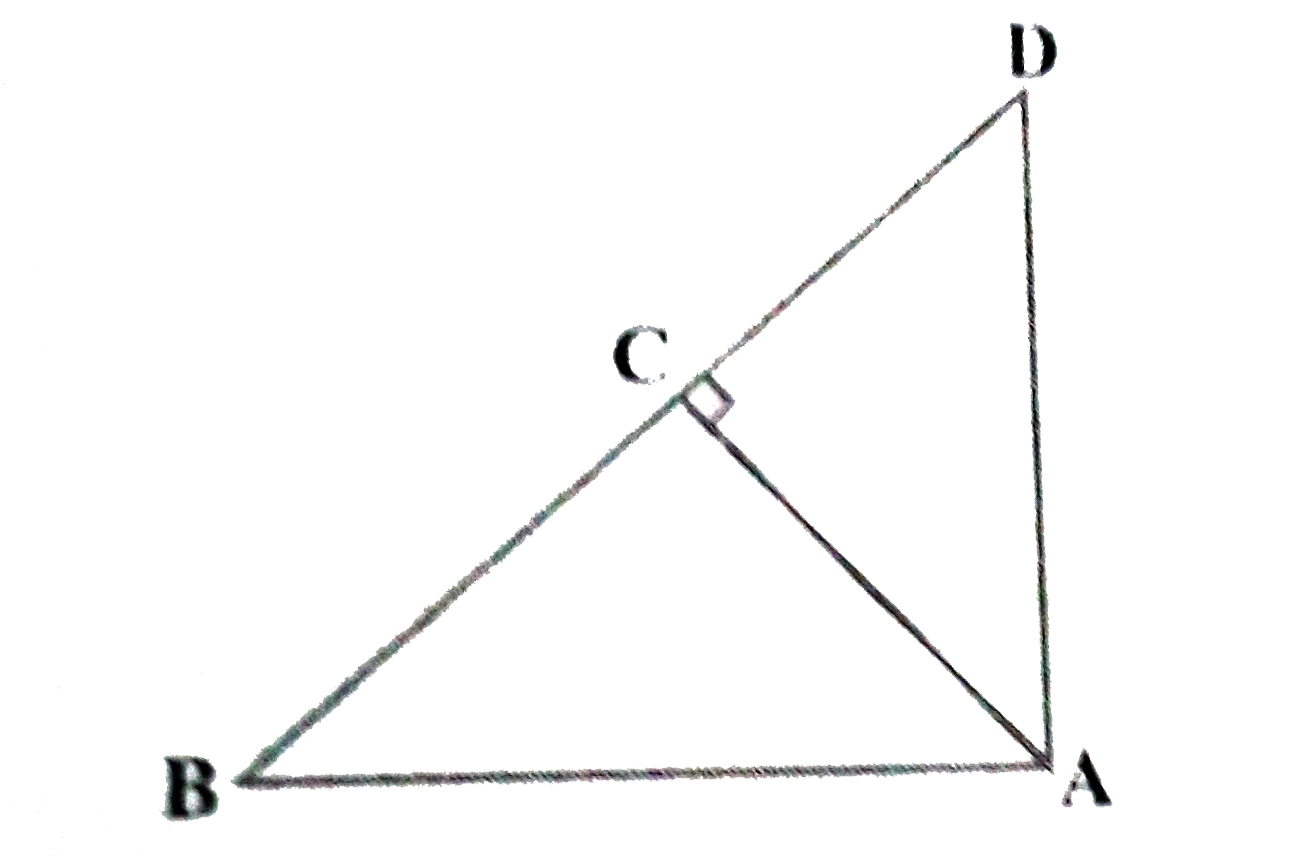
View SolutionIn Figure, ABD is a triangle right-angled at A and AC⊥BD. Show that
(i)AB2=BC.BD
(ii) AC2=BC.DC
(iii) AD2=BD.CD
View Solution
