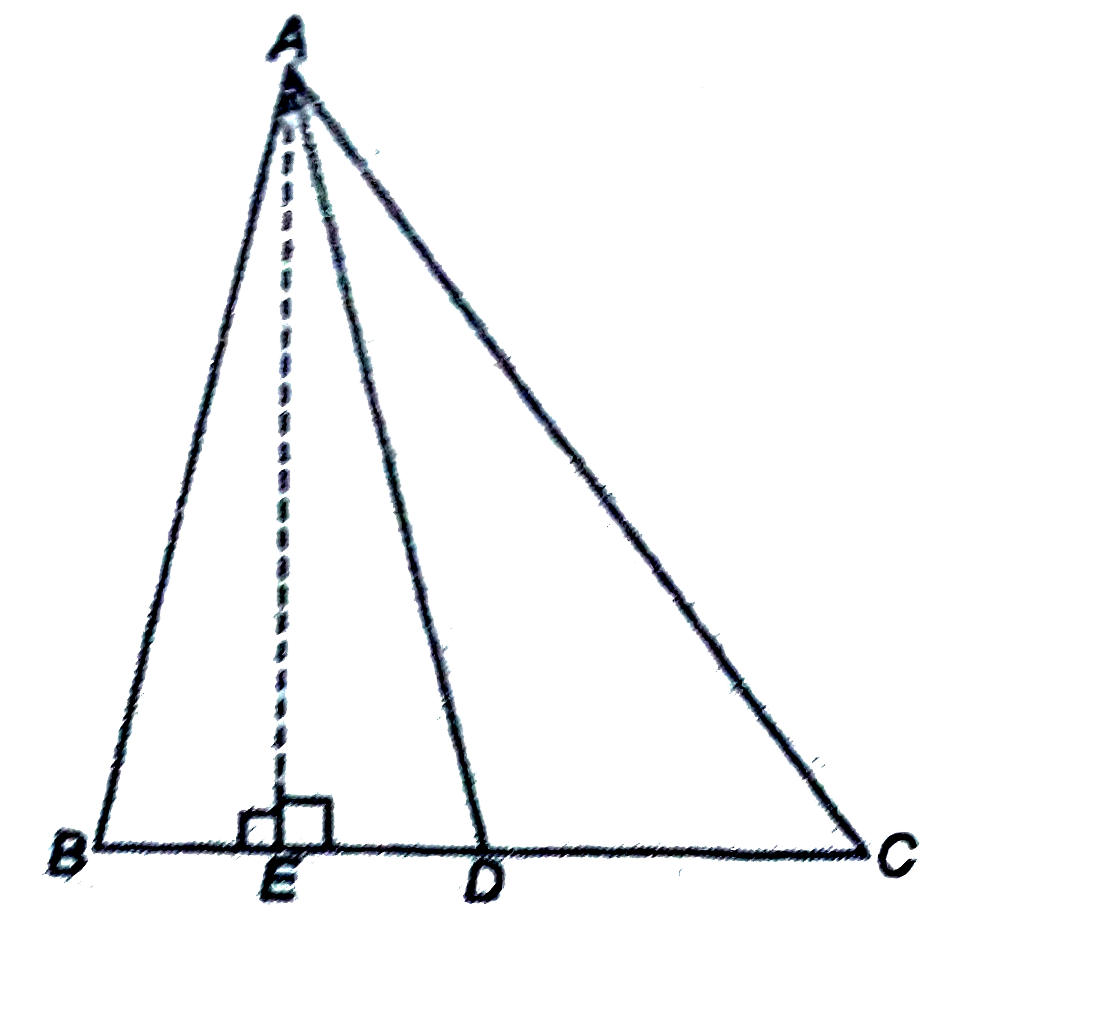
In a triangle ABC, AC>AB , D is the mid-point of BC and AE⊥BC . Prove that: (i) AB2=AD2−BC.DE+14BC2 (ii) AB2+AC2=2 AD2+12BC2
△ABC in which AD is the median , i.e. BD= DC = BC2
To prove : AB2+AC2=2AD2+12BC2
Construction: Draw AE⊥BC
Proof : L.H.S. = AB2+AC2
(AE2+BE2)+(AE2+EC2)
(by Pythagores theorem)
2AE2+BE2+EC2
2(AD2−DE2)+BD−ED)2)+(ED+DC)2
2AD2−2DE2+BD2+ED2−2BD.ED+ED2+DC2+2ED.DC
=2D2+(12BC)2−2BC2.ED+(12BC)2+2ED(BC2) (DB=DC=BC2
=2AD2+12BC2
R.H.S. Hence proved
Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar
14 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Exercise 6a
24 Videos
- STATISTICS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
4 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
In right-angled triangle ABC in which ∠C=90∘ , if D is the mid-point of BC , prove that AB2=4 AD2−3 AC2 .
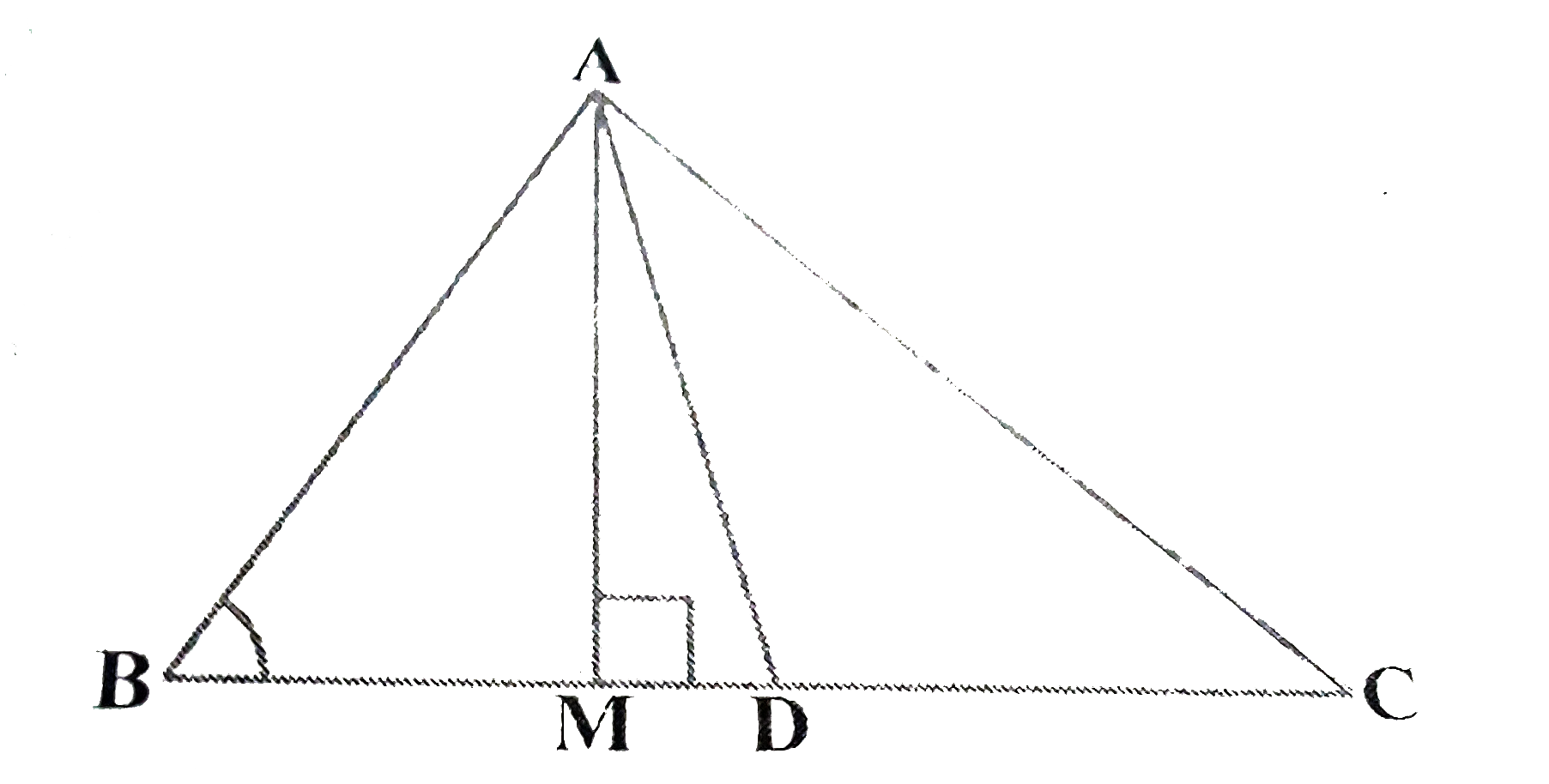
View SolutionIn figure, AD is a median of a triangle ABC and AM⊥BC. Prove that:
(i) AC2=AD2+BC.DM+(BC2)2
(ii) AB2=AD2−BC.DM+(BC2)2
(iii) AC2+AB2=2AD2+12BC2
View SolutionIn fig., if AD⊥BC, prove thatAB2+CD2=BD2+AC2.
View SolutionIn figure, ABC is a triangle in which ∠ABC=90∘and AD⊥BC. Prove that AC2=AB2+BC2−2BC.BD.

View SolutionIn a right ABC right-angled at C , if D is the mid-point of BC , prove that BC2=4 (AD2−AC2) .
View SolutionABC is a triangle in which AB=AC and D is any point in BC . Prove that AB2−AD2=BDCD .
View SolutionIn ABC , AD is perpendicular to BC . Prove that: AB2+CD2=AC2+BD2 (ii) AB2−BD2=AC2−CD2
View SolutionIn an isosceles triangle ABC with AB=AC , BD is perpendicular from B to the side AC . Prove that BD2−CD2=2 CDAD
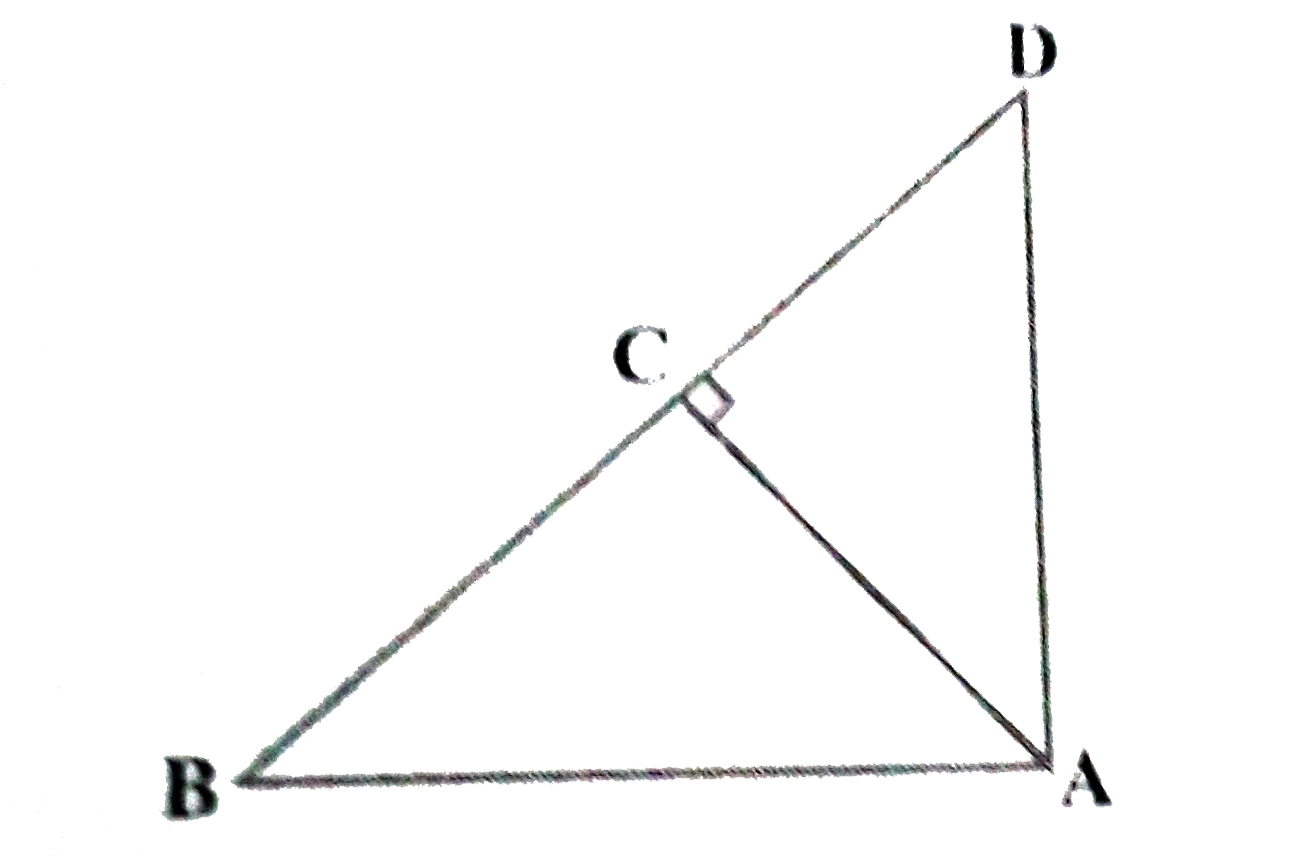
View SolutionIn Figure, ABD is a triangle right-angled at A and AC⊥BD. Show that
(i)AB2=BC.BD
(ii) AC2=BC.DC
(iii) AD2=BD.CD
View SolutionIn ABC , AD is a median. Prove that AB2+AC2=2 AD2+2 DC2 .
View Solution
