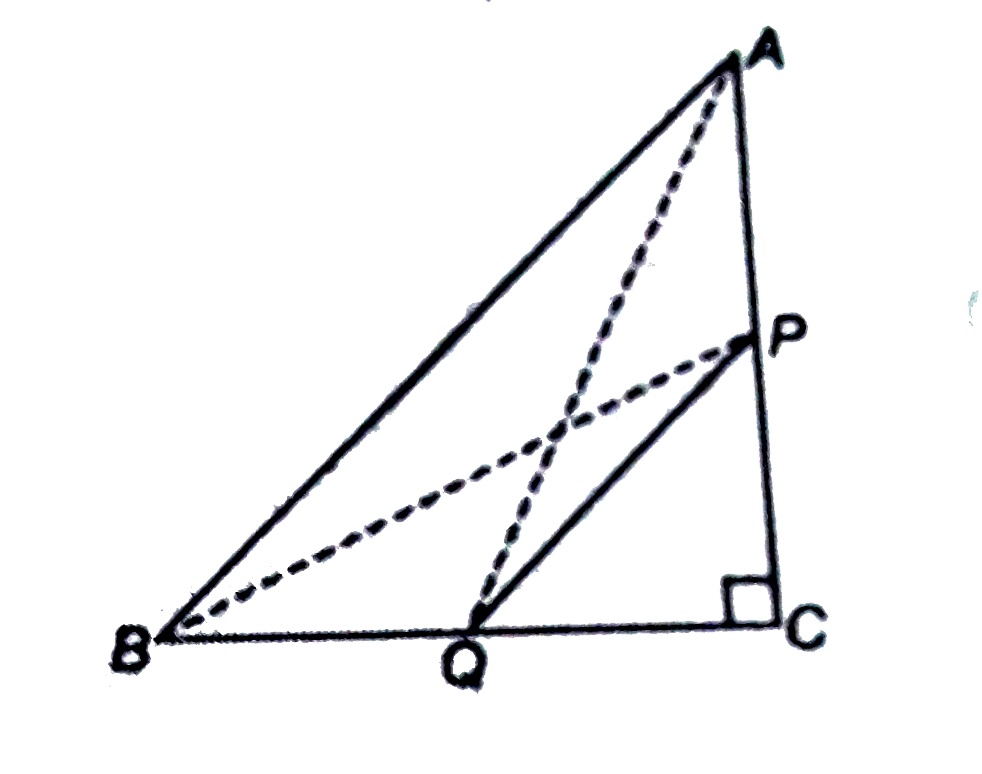
P and Q are the mid-points of the sides CA and CB respectively of a , right angled at C, prove that.
(i) (ii) (iii)
(i)
Using Pythagoras theorem
(Q is the mid-point of BC)
…(1) Hence proved.
(ii) ,
Using Pythagoras theorem, we have
,
(since P is the mid-point of AC)
...(2) Hence proved.
(iii) Adding (1) and (2) we get
Hence proved.
Topper's Solved these Questions
- TRIANGLES Book:NAGEEN PRAKASHAN ENGLISHChapter:TRIANGLES Exercise:Problems From NCERT/ Exemplar
Explore 14 Videos
- TRIANGLES Book:NAGEEN PRAKASHAN ENGLISHChapter:TRIANGLES Exercise:Exercise 6a
Explore 24 Videos
- STATISTICS Book:NAGEEN PRAKASHAN ENGLISHChapter:STATISTICS Exercise:Revision Exercise Long Answer Questions
Explore 4 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBook:NAGEEN PRAKASHAN ENGLISHChapter:VOLUME AND SURFACE AREA OF SOLIDSExercise:Revisions Exercise Long Answer Questions
Explore 5 Videos
Similar Questions
P and Q are the mid-points of the CA and CD respectively of a triangle ABC, right angled at C. Prove that: 4AQ2=4AC2+ BC2, 4BP2=4BC2+AC2, and 4(AQ2+ BP2)=5AB2.
View SolutionM and N are the mid-points of the sides QR and PQ respectively of a ΔPQR, right-angled at Q. Prove that :
(i) PM2+RN2=5MN2
(ii) 4PM2=4PQ2+QR2
(iii) 4RN2=PQ2+4QR2
(iv) 4(PM2+RN2)=5PR2
View SolutionIn △ABC,∠A=60∘ prove that BC2=AB2+AC2−AB.AC
View SolutionP and Q are points on the sides AB and AC respectively of a △ABC. If AP= 2cm, PB = 4cm AQ= 3cm and QC= 6cm. Show that BC= 3PQ.
View SolutionIf P and Q are points on the sides AB and AC respeactively of △ABC, if PQ||BC,l AP= 2 cm , AB = 6 cm and AC= 9 cm find AQ.
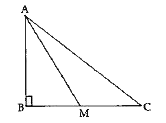
View SolutionABC is a triangle, right angled at B, M is a point on BC. Prove that :
AM2+BC2=AC2+BM2
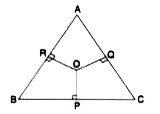
View SolutionIn the following figure, OP, OQ and OR are drawn perpendiculars to the sides BC, CA and AB repectively of triangle ABC. Prove that :
AR2+BP2+CQ2=AQ2+CP2+BR2
View SolutionIn a rhombus ABCD, prove that AC2+BD2=4AB2
View SolutionIn an acute angled triangle ABC, AD is the median in it. then :
AD2 =
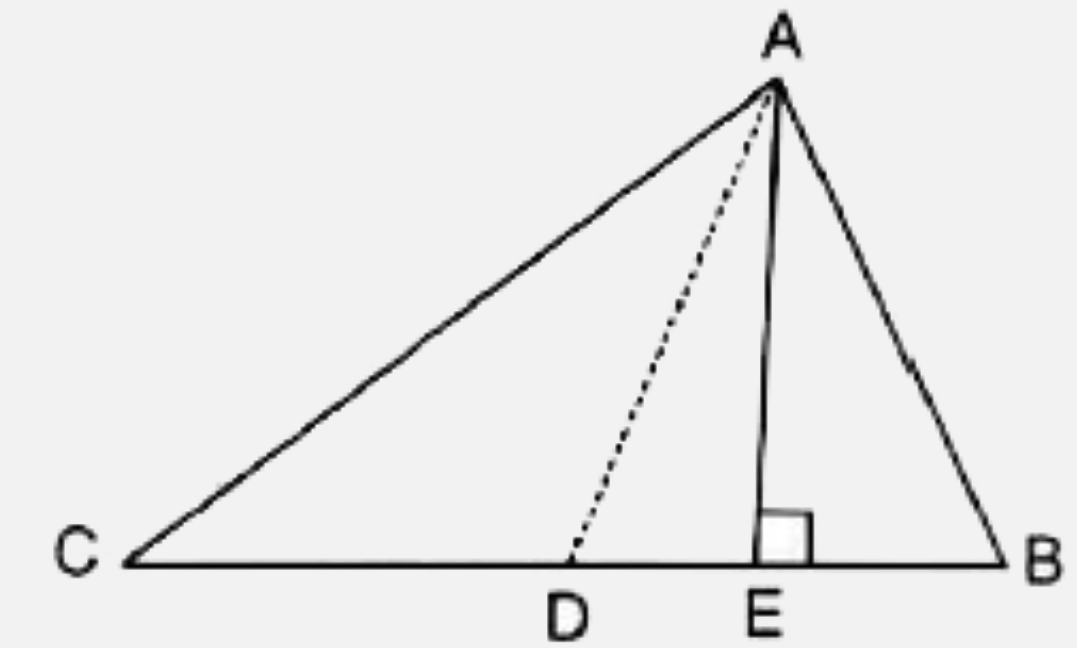
View SolutionThe following figures shows a triangle ABC in which AD is median and AE⊥BC.
Prove that : 2AB2+2AC2=4AD2+BC2
View Solution