Dr. Bansal needs to determine the distance PQ across a river in and east-west direction as shown in the adjoining figure. He can't measure this distance directly over the water. So, he selects the point S from where a straight line to point Q stays on land so he can mesure distance. he then moves eastward a distance of 400 m from point S to T , so that the line of sight from point T to P cuts the previous line SQ at R. finally with a long measuring tape. he determines that. SR = 250 m, QR= 1250 m
Determine if this is enough information to calculate the distance PQ and if so, find PQ and hence find the time taken by a swimmer to cross the river PQ with a uniform speed of 800 m/hr.

Video Solution

Text Solution

Verified by Experts

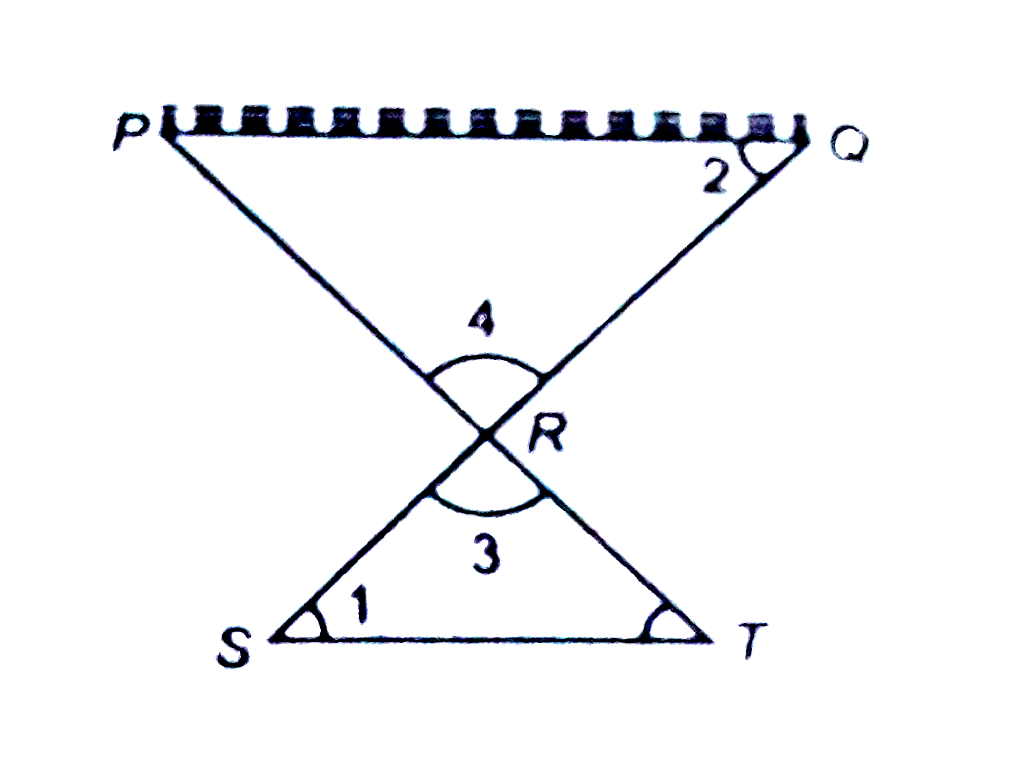
In $△ S R T and △ P Q R$
$∠ 3 = ∠ 4$ ( vertically oppostie angles)
$∠ 1 = ∠ 2$ ( alternate angles)
$△ S R T ~ △ Q R P$ ( AA corollary)
$\frac{S R}{Q R} = \frac{R T}{R P} = \frac{S T}{Q P}$ (corresponding sides of similar triangles are proportional)
( since he moves eastward, a distance of 400 m from point S )
$\Rightarrow P Q = \frac{400 \times 1250}{250} = 2000 m$
Hence, width of the river= 2000 m
A swimmer swims 800 m in 60min.
A swimmer swims 1 m in $\frac{60}{800}$ min
A swimmer swims 2000 m in $\frac{60}{800} \times 2000 min$
150 min = 2 hr and 30 minutes.

Updated on:21/07/2023