In the given figure if ∠B=90∘ and BD is perpendicular to AC then
prove that:
(i)△ADB~△BDC(ii)△ADB~△ABC
(iii) △BDC~△ABC(iv)BD2=AD×DC
(v) AB2=AD×AC(vi)BC2=CD×AC
(vii) AB2+BC2=AC2

(i) In △ADBand△BDC
∠5=∠4 (each 90∘)Searching for second AnglesWe know that ∠1+∠2=90∘.....(1)Also, Since ∠4=90∘∴ ∠2+∠3=90∘ (angle sum property)...(2)∴From (1) and (2) , We get ⇒ ∠1+∠2=∠2+∠3 (each90∘)⇒ ∠1=∠3
∠1=∠3 ( just proved)
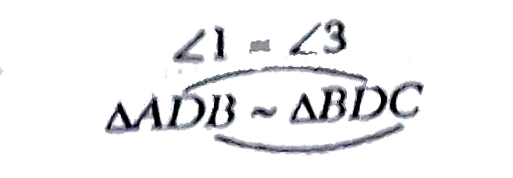 (AA corollary) Hence proved.
(AA corollary) Hence proved.
(ii) △BDCand△ABC
∠4=∠1+∠2(each90∘)
∠3=∠3 ( common)
 (AA corollary) Hence poved.
(AA corollary) Hence poved.
(iii) In △BDCandtr∈∠ABC
∠4=∠1+∠2(each90∘)
∠3=∠3 (common)
 [from part (i)
[from part (i)
(corresponding sides of similar triangles are proportional)
(iv) For BD2=AD×DC . we need to prove two △s similar which contain BD, AD and DC as sides.
Obviosly these are △ABDand△BDC, we have proved these △s as similar in part (i). so ,
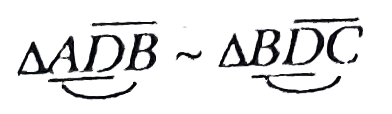 [from part (ii)]
[from part (ii)]
( corresponding sides of similar triangle are proportional)
BD2=AD×DC Hence proved.
(v) For AB2=AD×AC we need to prove two triangles similar which contain AB, AD and AC as sides. Obviosusly these are △ABDand△ABC. we have already proved these △s as similar in part (ii)
△ADB~△ABC [ from part (ii) ]
⇒AB2=AD×AC .... (1) Hence proved
(vi) For BC2=CD×AC we need to prove two triangles similar which contains BC, CD and AC as sides. Obviosly these are △BDCand△ABC , we have proved these triangles as similar in part (iii)
so,
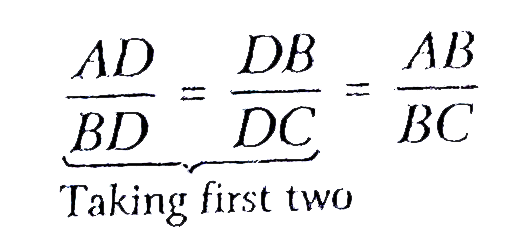 ( cossesponding sides of similar triangle are proportional)
( cossesponding sides of similar triangle are proportional)
BC2=CD×AC ....(2) Hence proved.
(vii) Addings results (1) and (2), we get
AB2+BC2=AD×AC+CD×AC
AC(AD+CD)<br>=AC×AC=AC2 Hence proved.
Topper's Solved these Questions
- TRIANGLES Book:NAGEEN PRAKASHAN ENGLISHChapter:TRIANGLES Exercise:Problems From NCERT/ Exemplar
Explore 14 Videos
- TRIANGLES Book:NAGEEN PRAKASHAN ENGLISHChapter:TRIANGLES Exercise:Exercise 6a
Explore 24 Videos
- STATISTICS Book:NAGEEN PRAKASHAN ENGLISHChapter:STATISTICS Exercise:Revision Exercise Long Answer Questions
Explore 4 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBook:NAGEEN PRAKASHAN ENGLISHChapter:VOLUME AND SURFACE AREA OF SOLIDSExercise:Revisions Exercise Long Answer Questions
Explore 5 Videos
Similar Questions
In the given figure, ∠ABC=90∘ and BC is diameter of the given circle. Show that:
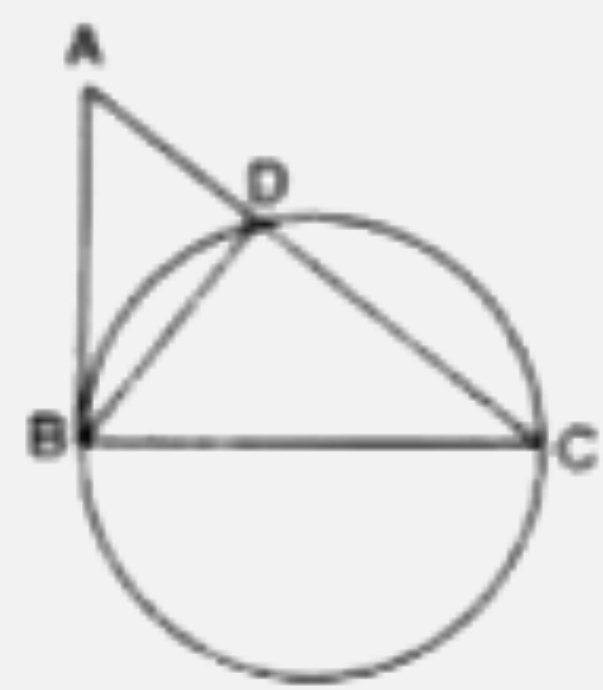
AC×AD=AB2
View SolutionIn the given figure, ∠ABC=90∘ and BC is diameter of the given circle. Show that:

AC×CD=BC2
View SolutionIn the figure AB = BC and AD is perpendicular to CD. Prove that :
AC2=2.BC.DC
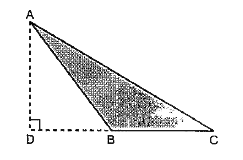
View SolutionIn triangle ABC, AB=AC and BD is perpendicular to AC. Prove that : BD2−CD2=2CD×AD
View SolutionIn the figure, AD is perpendicular to BC, prove that AB+AC>2AD.

View SolutionIn the given figure AC = BD, prove that AB = CD.

View SolutionIn a triangle ABC,B=90∘ and D is the mid-oint of BC then prove that AC2=AD2+3CD2
View SolutionIn triangles ABC , AD is perpendicular to BC and AD2=BD×DC . Prove that angle BAC=90∘
View SolutionThe following figure shows a trapezium ABCD in which AB is parallel to DC and AD = BC.
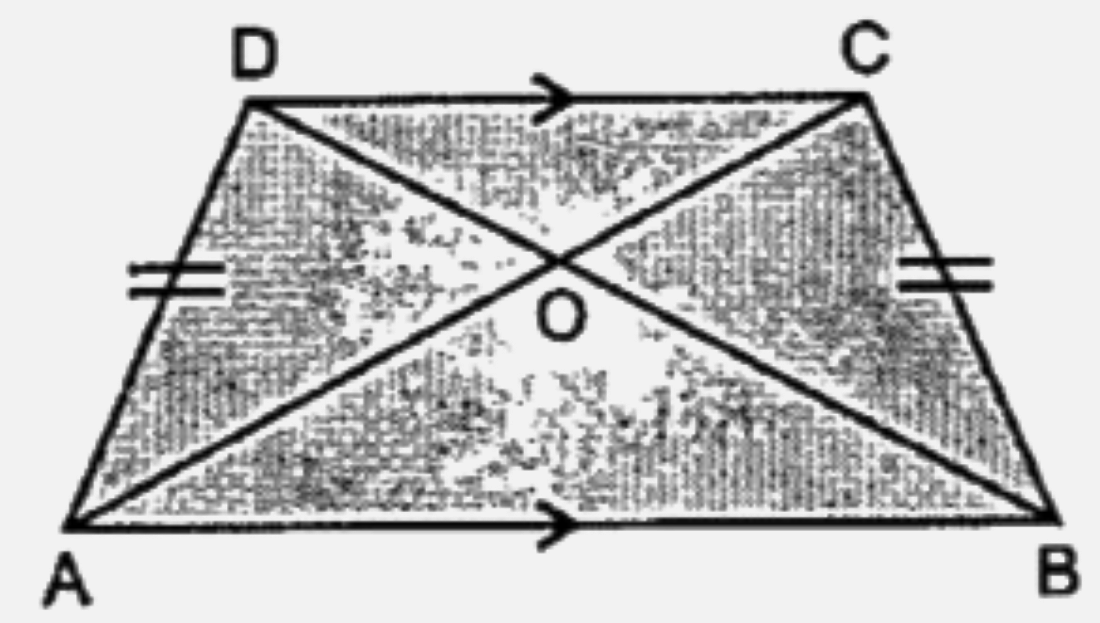
Prove that :
(i) ∠DAB=∠CBA
(ii) ∠ADC=∠BCD
(iii) AC = BD
(iv) OA = OB and OC = OD
View Solutionin the given figure ∠CAB=90∘andAD⊥BC. if AC= 75 cm , AB= 1m and BD= 1.25 m . Find AD.

View Solution

