Question

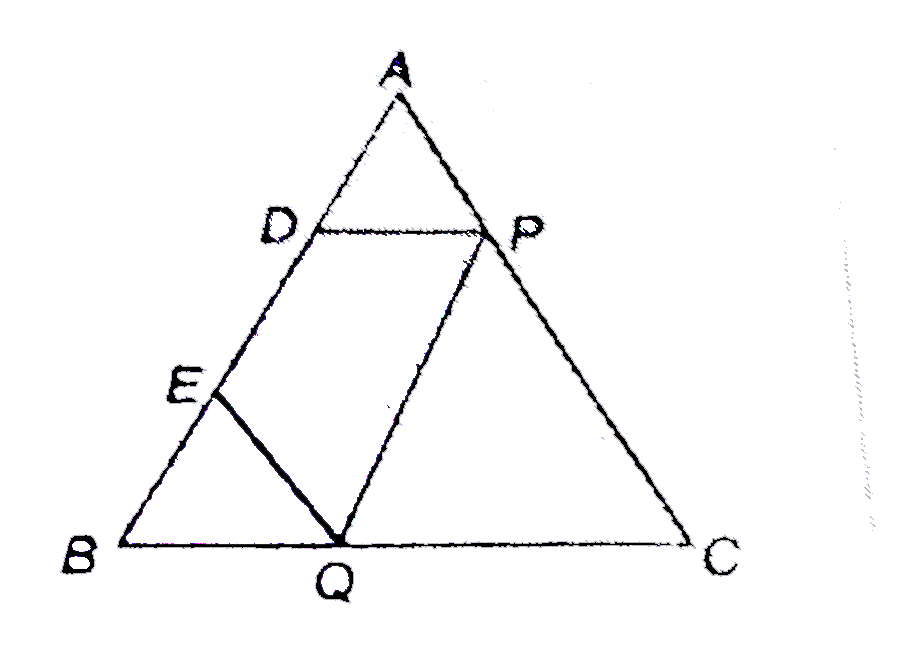
Let $ABC$
be a triangle and $D\text{and}E$
be two points on side $AB$
such that $AD=BE$.
If $DP\mid \mid BC$
and $EQ\mid \mid AC,$
Then prove that $PQ\mid \mid AB$.

Explanation

`DeltaABC` in which D and E are two points such that AD=BE.
Also DP||BC and EQ||AC.
To Prove : PQ||AB
Proof: In `DeltaABC`Since DP|| BC.
` (AB)/(EA) =(BQ)/(QC)`
In `DeltaABC` since EQ||AC
`(BE)/(EA) =(BQ)/(QC)`
Now, as AD=BE
AD+DE= BE+DE
AE=BD (adding DE on both sides)
AE=BD ....(4)
From (1) (2) (3) and (4)
`(AP)/(PC)= (BQ)/(QC)`
PQ||AB ( by the converse of B.P. theroem) Hence proved.