Question

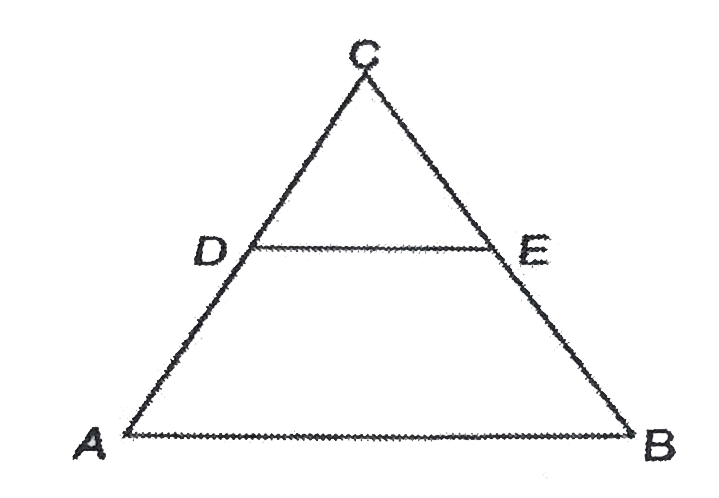
In the given figure, in $\Delta ABC,DE\mid \mid BC$ so that AD= (4x - 3) cm, AE= ( 8x-7) cm, BD= (3x-1) cm and CE= (5x-3) cm . Find the value of x.

Explanation

To solve the problem, we will use Thales' theorem, which states that if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally.

Given:
- AD = (4x - 3) cm
- AE = (8x - 7) cm
- BD = (3x - 1) cm
- CE = (5x - 3) cm

Since DE || BC, we can apply Thales' theorem:

$$\frac{AD}{BD}=\frac{AE}{CE}$$

Substituting the given values into the equation:

$$\frac{4x-3}{3x-1}=\frac{8x-7}{5x-3}$$

Next, we will cross-multiply to eliminate the fractions:

$$(4x-3)(5x-3)=(8x-7)(3x-1)$$

Now, we will expand both sides of the equation:

Left side:
$$(4x-3)(5x-3)=20x^2-12x-15$$

Right side:
$$(8x-7)(3x-1)=24x^2-8x-21$$

Now we set the two expanded expressions equal to each other:

$$20x^2-12x-15=24x^2-8x-21$$

Next, we will move all terms to one side of the equation to set it to zero:

$$20x^2-12x-15-24x^2+8x+21=0$$

Combining like terms:

$$-4x^2-4x+6=0$$

To simplify, we can multiply the entire equation by -1:

$$4x^2+4x-6=0$$

Now, we can divide the entire equation by 2 to simplify further:

$$2x^2+2x-3=0$$

Next, we will use the quadratic formula to find the values of x, where $$a=2,b=2,c=-3$$:

$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$

Calculating the discriminant:

$$b^2-4ac=2^2-4\left(2\right)(-3)=4+24=28$$

Now substituting back into the quadratic formula:

$$x=\frac{-2\pm \sqrt{28}}{4}$$

Simplifying $$\sqrt{28}$$:

$$\sqrt{28}=2\sqrt{7}$$

So,

$$x=\frac{-2\pm 2\sqrt{7}}{4}=\frac{-1\pm \sqrt{7}}{2}$$

Thus, the possible values of x are:

$$x=\frac{-1+\sqrt{7}}{2}\text{or}x=\frac{-1-\sqrt{7}}{2}$$

Since x must be a positive length, we take:

$$x=\frac{-1+\sqrt{7}}{2}$$