In , find c.
To find the length of side c in triangle ABC where a=x2−1, b=2x+1, and ∠C=120∘, we can use the Law of Cosines. The Law of Cosines states that:
c2=a2+b2−2ab⋅cos(C)
1. Identify the values:
- a=x2−1
- b=2x+1
- ∠C=120∘
2. Calculate cos(120∘):
cos(120∘)=−12
3. Substitute the values into the Law of Cosines:
c2=(x2−1)2+(2x+1)2−2⋅(x2−1)(2x+1)⋅(−12)
4. Expand (x2−1)2:
(x2−1)2=x4−2x2+1
5. Expand (2x+1)2:
(2x+1)2=4x2+4x+1
6. Combine the expansions:
c2=(x4−2x2+1)+(4x2+4x+1)+(x2−1)(2x+1)
7. Calculate (x2−1)(2x+1):
(x2−1)(2x+1)=2x3+x2−2x−1
8. Substituting back into the equation:
c2=x4−2x2+1+4x2+4x+1+(−12)(2x3+x2−2x−1)
9. Simplify the equation:
c2=x4+2x2+2+4x−(x3+12x2−x−12)
=x4+2x2+2+4x−x3−12x2+x+12
=x4−x3+(2x2−12x2)+(4x+x)+(2+12)
=x4−x3+32x2+5x+52
10. Final expression for c2:
c2=x4+2x3+3x2+5x+5
11. Taking the square root to find c:
c=√x4+2x3+3x2+5x+5
Final Answer:
c=x2+x+1
- a=x2−1
- b=2x+1
- ∠C=120∘
cos(120∘)=−12
c2=(x2−1)2+(2x+1)2−2⋅(x2−1)(2x+1)⋅(−12)
(x2−1)2=x4−2x2+1
(2x+1)2=4x2+4x+1
c2=(x4−2x2+1)+(4x2+4x+1)+(x2−1)(2x+1)
(x2−1)(2x+1)=2x3+x2−2x−1
c2=x4−2x2+1+4x2+4x+1+(−12)(2x3+x2−2x−1)
c2=x4+2x2+2+4x−(x3+12x2−x−12)
=x4+2x2+2+4x−x3−12x2+x+12
=x4−x3+(2x2−12x2)+(4x+x)+(2+12)
=x4−x3+32x2+5x+52
c2=x4+2x3+3x2+5x+5
c=√x4+2x3+3x2+5x+5
c=x2+x+1
Topper's Solved these Questions
- TRIGNOMETRIC FUNCTIONSBook:NAGEEN PRAKASHAN ENGLISHChapter:TRIGNOMETRIC FUNCTIONSExercise:EXERCISES 3O
Explore 24 Videos
- TRIGNOMETRIC FUNCTIONSBook:NAGEEN PRAKASHAN ENGLISHChapter:TRIGNOMETRIC FUNCTIONSExercise:EXERCISES 3P
Explore 32 Videos
- TRIGNOMETRIC FUNCTIONSBook:NAGEEN PRAKASHAN ENGLISHChapter:TRIGNOMETRIC FUNCTIONSExercise:EXERCISES 3M
Explore 8 Videos
- STRAIGHT LINESBook:NAGEEN PRAKASHAN ENGLISHChapter:STRAIGHT LINESExercise:Exercise
Explore 207 Videos
Similar Questions
Knowledge Check
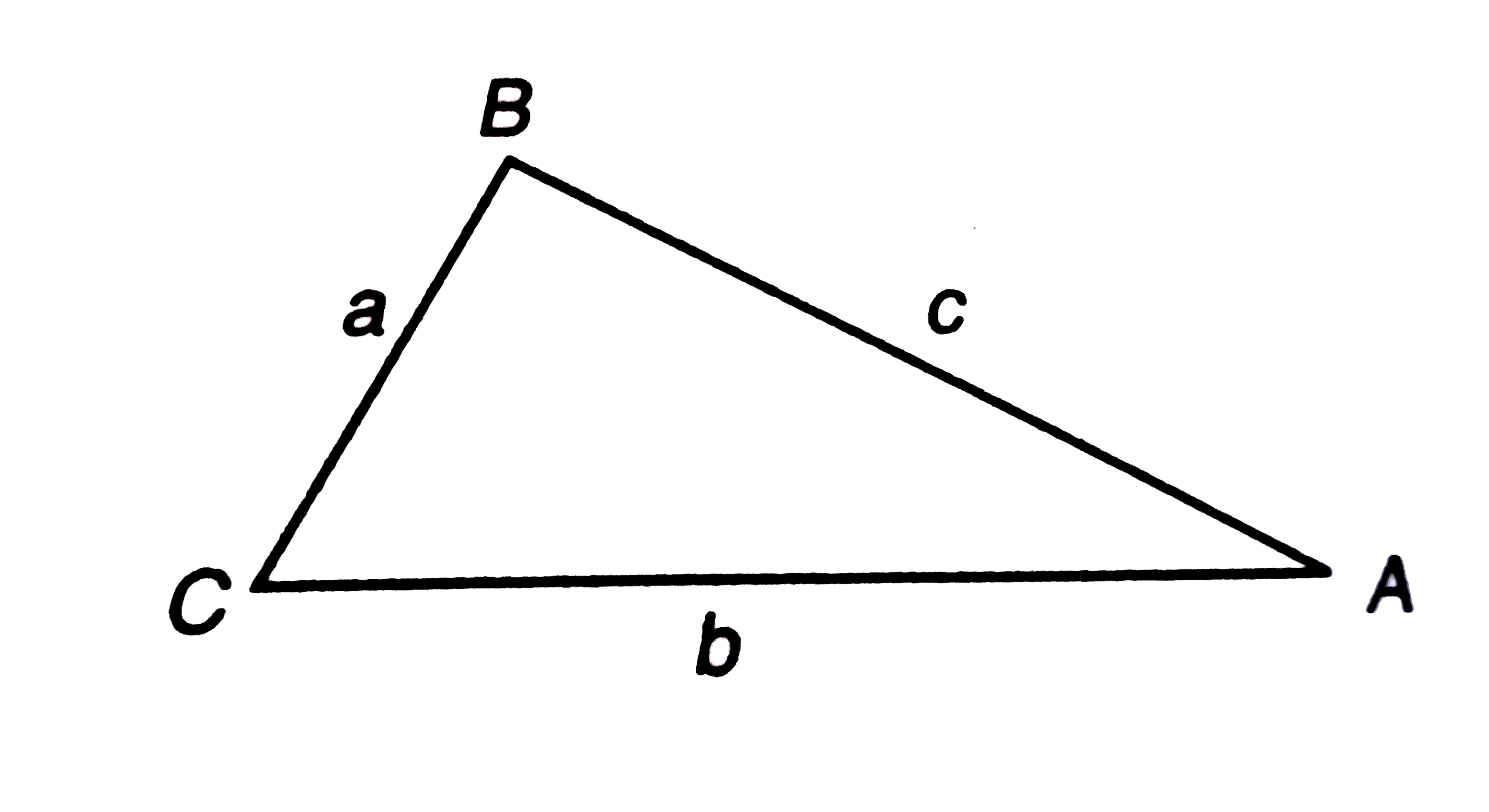
In △ABC above, a=2x, b=3x+2, c=√12, and ∠C=60∘. Find x.A0.50B0.64C0.77D1.64
In ΔABC,∠A=x+15∘,∠B=xand∠C=2x−35∘ find, each angle of the triangle.
View SolutionIn ΔABC,b=2√3,c=3√2,∠C=60∘, evaluate ∠A.
View SolutionIn a ΔABC,∠A=2∠B=3∠C, find each of the triangle.
View SolutionIn ΔABC,∠A=2πc3 and ∠B=45∘. Find ∠C in both the systems.
View SolutionIn ΔABC, if ∠C=90∘, then a+cb+b+ca is equal to :
View SolutionIn a ΔABC, if c = 2, A=120∘,a=√6, then C=
View SolutionIn ΔABC,∠C=90∘andtanA=1√3,find the value of sin A cosB+cosAsinB.
View Solution

