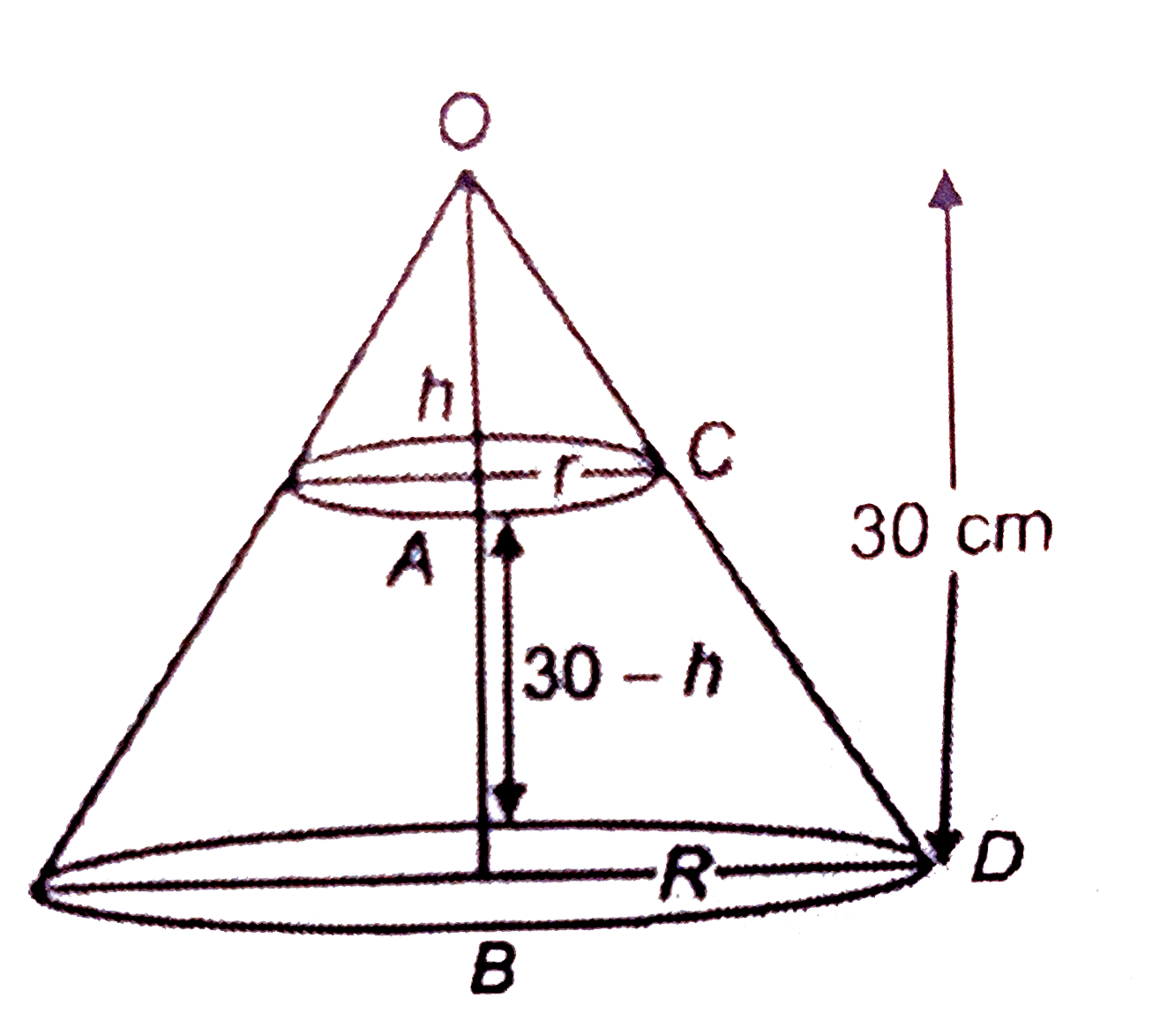
The height of a cone is 30 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume be $\frac{1}{27}$ of the volume of the given cone, at what height above the base is the section mode?

Video Solution

Text Solution

Verified by Experts

Let OA=h $\Rightarrow$ AB=30-h
and let AC=r,BD=R
$△$ OAC $△$ OBD
$\frac{h}{30} = \frac{r}{R} \Rightarrow r = \frac{h R}{30}$
Now volume of smaller cone = $\frac{1}{27} \times$ volume of larger cone
$\frac{1}{3} π r^{2} h = \frac{1}{27} \times \frac{1}{3} \times (π R^{2} \times 30$
$\frac{1}{3} π \frac{h r}{{(30)}^{2}} . h = \frac{1}{27} \times \frac{1}{3} π R^{2} \times 30$
$\frac{h^{2}}{30^{2}} = \frac{30}{2} \Rightarrow h^{3} = \frac{30^{3}}{30^{3}} \Rightarrow h = 10$
Required height =30-10=20 cm
1kl= $1 m^{3}$
1000= $1000 \times 100 \times 100 c m^{3}$
1 litre =1000 $c m^{3}$
1cm $5^{3} = \frac{1}{1000}$ litre

|

Updated on:21/07/2023

Class 10 MATHS SURFACE AREAS AND VOLUMES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The height of a cone is equal to the radius of its base. The radius of a sphere is equal to the radius of the base of the cone. The ratio of the volume of the cone to the volume of the sphere is
A $\frac{1}{12}$
B $\frac{1}{4}$
C $\frac{1}{3}$
D $\frac{1}{1}$

NAGEEN PRAKASHAN ENGLISH-VOLUME AND SURFACE AREA OF SOLIDS-Revisions Exercise Long Answer Questions

Home
Ask Doubt
Profile