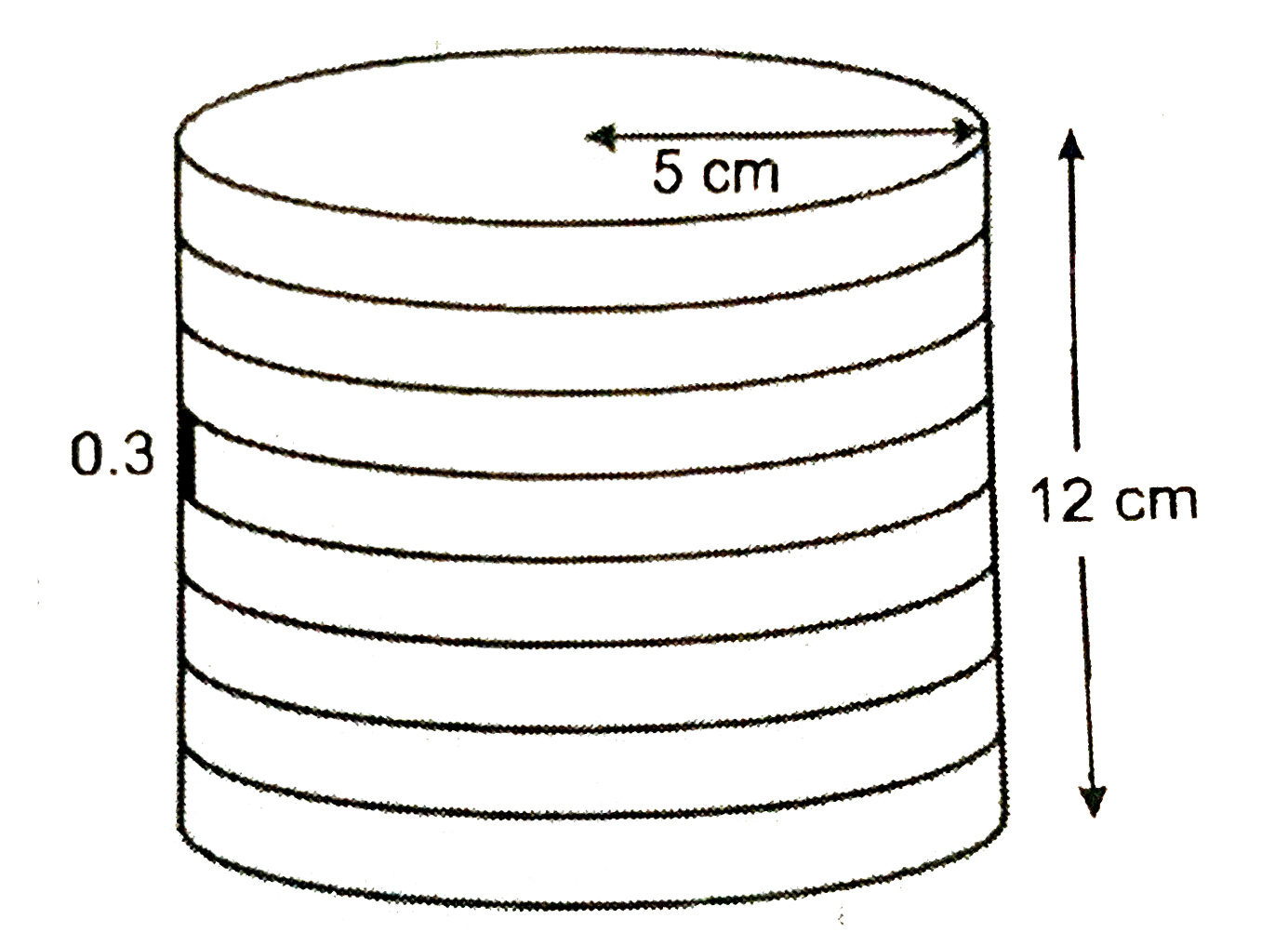
A copper wire, 3 mm in diameter, is wound about a cylinder whose length is 12 cm, and diameter 10 cm, so as to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of copper to be 8.88 g per cm3
The correct Answer is:19093 cm3
(i) Let the wire wounded around the cylinder completes n revolutions.
Diameter (width) of wire = 3m=0.3 cm
So whole height of cylinder =0.3 n cm
But whole height of cylinder =12 cm
0.3 n=12→n=120.3=1203=40
So 40 revolutions are completed to wound the wire completely on the cylinder
In I revolution length of wire = 2 πr
In 40 revolutions length of wire =40×2πr
=80×227×5cm=1257.14cm
=12.57 m.(ii) Now radius of wire=0.32=0.15cm
volume of wire =area of cross section× length of wire
=π(0.15)2×1257.14=88.898cm3
Mass of wire = volume × density
=88.898×8.88 g=789.41 g
Hence length of wire = 12.57 m
and mass of wire =789.41 g
Topper's Solved these Questions
- VOLUME AND SURFACE AREA OF SOLIDSBook:NAGEEN PRAKASHAN ENGLISHChapter:VOLUME AND SURFACE AREA OF SOLIDSExercise:Problems From NCERT/exemplar
Explore 10 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBook:NAGEEN PRAKASHAN ENGLISHChapter:VOLUME AND SURFACE AREA OF SOLIDSExercise:Exercise
Explore 68 Videos
- TRIANGLES Book:NAGEEN PRAKASHAN ENGLISHChapter:TRIANGLES Exercise:Revision Exercise Long Questions
Explore 1 Video
Similar Questions
A copper wire of diameter 6mm is evenly wrapped on the cylinder of length 18cm and diameter 49cm to cover the whole surface. Find:
the volume of the wire.
View SolutionA copper wire of diameter 6mm is evenly wrapped on the cylinder of length 18cm and diameter 49cm to cover the whole surface. Find:
the length
View SolutionA copper wire of diameter 6 mm is evenly wrapped on a cylinder of length of length 15 cm and diameter 49 cm to cover its volume surface. Find the length and volume of wire. If the specific gravity of copper be 9g per cubic cm. Find the weigth of the wire.
View SolutionFind the height of the cylinder whose volume is 154m3 and diameter of the base is 140cm ?
View SolutionA cylinder of same height and radius is placed on the top of a hemisphere. Find the curved surface area of the shape if the length of the shape by 7cm.
View SolutionThe diameter of a metallic ball is 4.2 cm. What is the mass of the ball, if the density of the metal is 8.9 g per cm3?
View SolutionA cylinder has a diameter of 20 cm. The area of the curved surface is 100 cm2. Find the volume of the cylinder (in. cm3).
View SolutionThe diameter of a sphere is 6 cm. It is melted and drawn into a wire of diameter 0-2 cm. Find the length of the wire.
View SolutionFind the length of 13.2 kg of copper wire of diameter 4mm, when 1 cubic cm of copper weights 8.4 gm.
View SolutionFind the length of 13.2 kg of copper wire of diameter 4mm, when 1 cubic cm of copper weights 8.4 gm.
View Solution