A semicircle of radius 17.5 cm is ratiatied about its diameter. Find the curved surface of so generated solid
The correct Answer is:136cm3
To find the curved surface area of the solid generated by rotating a semicircle about its diameter, we can follow these steps:
1. Identify the radius of the semicircle:
Given that the radius r of the semicircle is 17.5 cm.
2. Calculate the diameter:
The diameter d of the semicircle can be calculated using the formula:
d=2r
Substituting the value of r:
d=2×17.5=35 cm
3. Understand the shape formed:
When the semicircle is rotated about its diameter, it forms a solid known as a hemisphere.
4. Curved surface area formula:
The formula for the curved surface area A of a hemisphere is given by:
A=2πr2
5. Substitute the radius into the formula:
We substitute r=17.5 cm into the formula:
A=2π(17.5)2
6. Calculate (17.5)2:
(17.5)2=306.25
7. Substitute back into the area formula:
A=2π×306.25
A=612.5π
8. Use π≈227 for calculation:
A≈612.5×227
9. Calculate the area:
A≈612.5×3.14≈1925.625 cm2
10. Final Result:
The curved surface area of the solid generated by rotating the semicircle about its diameter is approximately:
A≈1925.63 cm2
Given that the radius r of the semicircle is 17.5 cm.
The diameter d of the semicircle can be calculated using the formula:
d=2r
Substituting the value of r:
d=2×17.5=35 cm
When the semicircle is rotated about its diameter, it forms a solid known as a hemisphere.
The formula for the curved surface area A of a hemisphere is given by:
A=2πr2
We substitute r=17.5 cm into the formula:
A=2π(17.5)2
(17.5)2=306.25
A=2π×306.25
A=612.5π
A≈612.5×227
A≈612.5×3.14≈1925.625 cm2
The curved surface area of the solid generated by rotating the semicircle about its diameter is approximately:
A≈1925.63 cm2
Topper's Solved these Questions
- VOLUME AND SURFACE AREA OF SOLIDSBook:NAGEEN PRAKASHAN ENGLISHChapter:VOLUME AND SURFACE AREA OF SOLIDSExercise:Problems From NCERT/exemplar
Explore 10 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBook:NAGEEN PRAKASHAN ENGLISHChapter:VOLUME AND SURFACE AREA OF SOLIDSExercise:Exercise
Explore 68 Videos
- TRIANGLES Book:NAGEEN PRAKASHAN ENGLISHChapter:TRIANGLES Exercise:Revision Exercise Long Questions
Explore 1 Video
Similar Questions
A semi-circle of radius 17.5 cm is rotated about its diameter. Find the curved surface of so generated solid.
View SolutionIn Fig. 12.33, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
View SolutionIn Fig. 12.33, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
View SolutionThe area of the base of a conical solid is 38.5cm2 and its volume is 154cm3. Find the curved surface area of the solid.
View SolutionA right triangle with sides 6 cm, 8 cm and 10 cm is revolved about the side 8 cm. Find the volume and the curved surface of the solid so formed.
View SolutionThree semicircles each of diameter 3 cm, a circle of diameter 4.5 cm and a semicircle of radius 4.5 cm are drawn in the adjoining figure. Find the area of the shaded region.
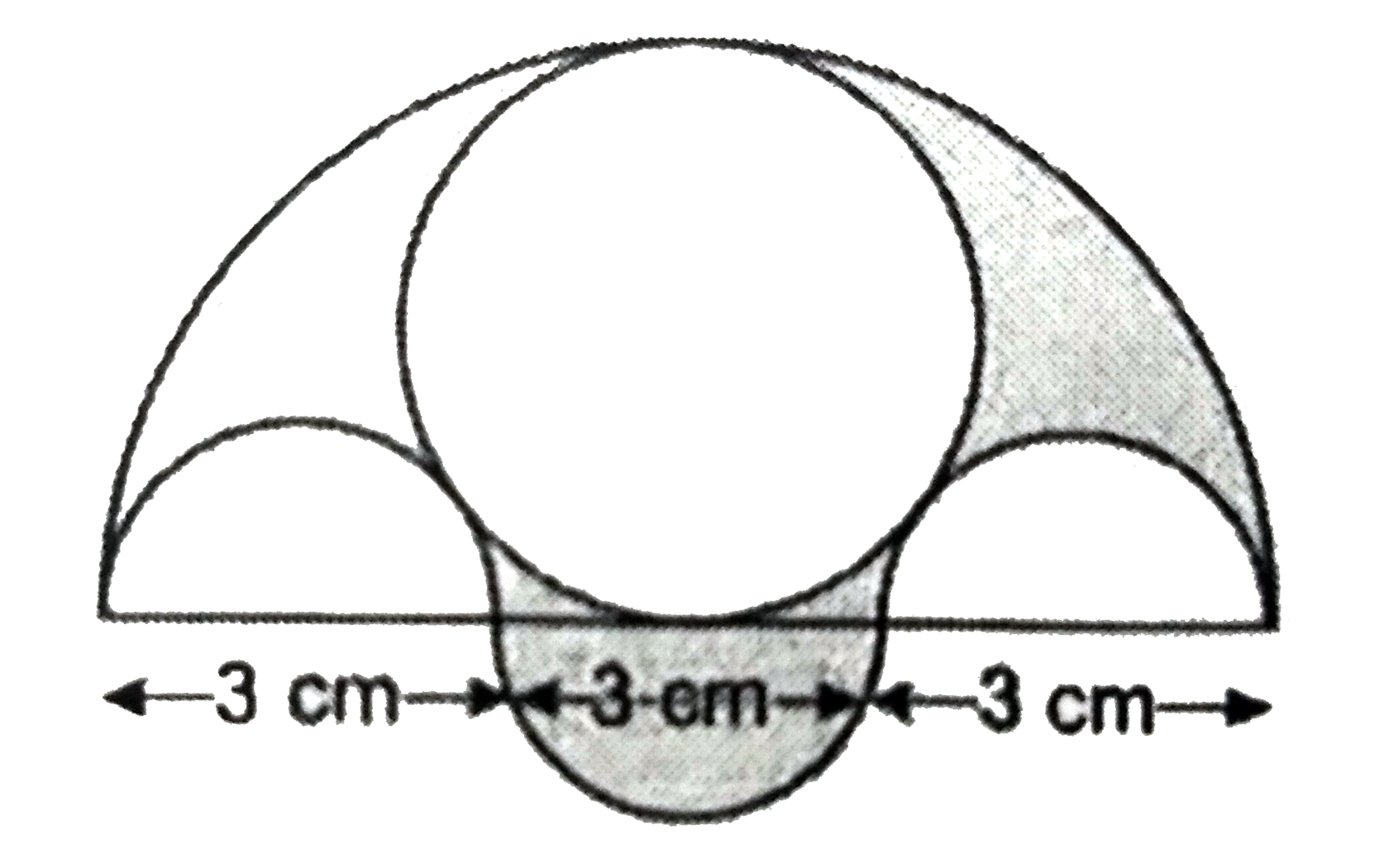
View SolutionABCP is a quadrant of a circle of radius 14 cm. with AC as diameter, a semicircle is drawn. Find the area of the shaded portion
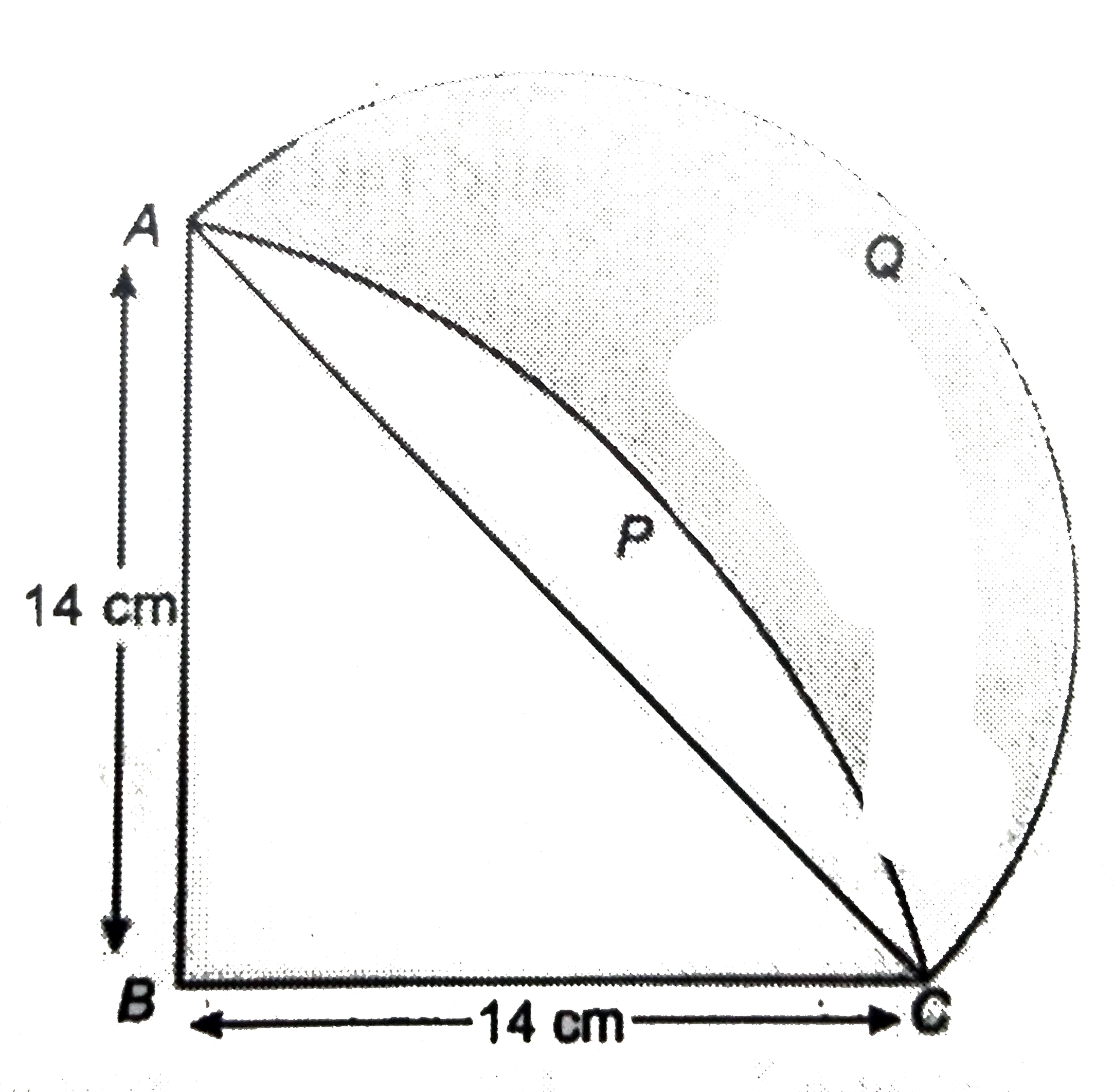
View SolutionThe surface area of a sphere of radius 5 cm is five times the curved surface area of a cone of radius 4 cm. Find the height and volume (correct to two decimal places) of the cone.
View SolutionThree semicircles each of diameter 3 cm, a circle of diameter 4·5 cm and a semicircle of radius 4·5 cm are drawn in the given figure. Find the area of the shaded region.
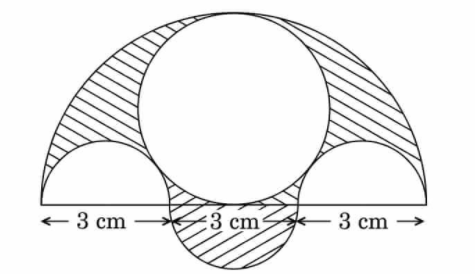
View SolutionThree semicircles each of diameter 3 cm, a circle of diameter 4·5 cm and a semicircle of radius 4·5 cm are drawn in the given figure. Find the area of the shaded region.

View Solution
