Three spheres of radius 'r' are kept inside a cuylinder such that two of the speres are at bottom touching each other and sides of the cylinder while the third sphere is touching the two bottom spheres and the top of the cylinder .Find the volume of the cylinder .
By Pythagoras theorem,
AM=r(√3)
Height of cylinder H=r+r(√3)+r→r(2+(√3))
Radius of cylinder R= 2r
Volume of cylinder =πR2H
=π(2r2).r(2+(√3))=4πr3(2+(√3))
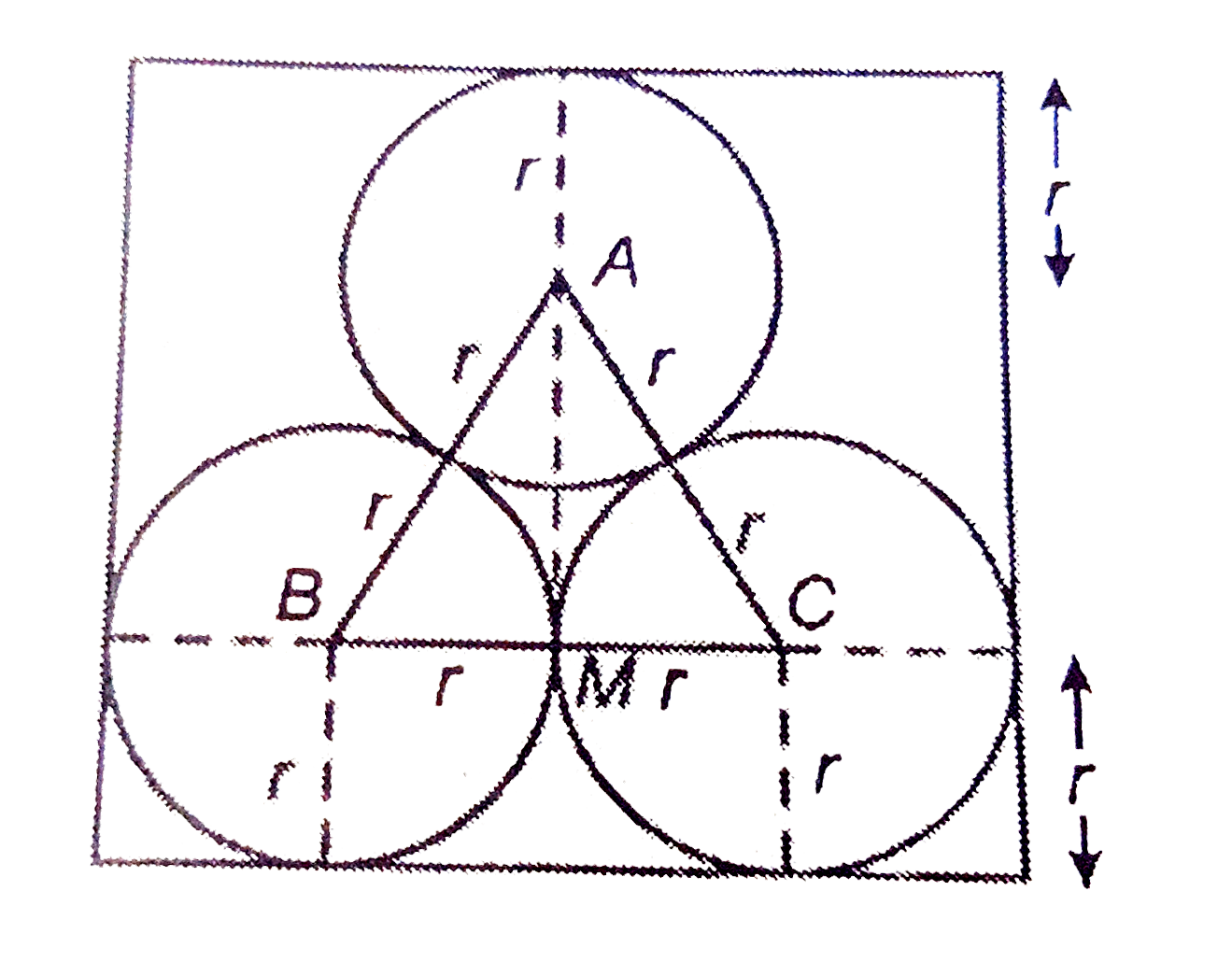
Related Playlists
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Problems From NCERT/exemplar10videos
VOLUME AND SURFACE AREA OF SOLIDS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Exercise68videos
VOLUME AND SURFACE AREA OF SOLIDS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Revision Exercise Long Questions1videos
TRIANGLES
Similar Questions
The radius and height of a cylinder are equal. If the radius of the sphere is equal to the height of the cylinder, then the ratio of the rates of increase of the volume of the sphere and the volume of the cylinder, is
View SolutionA sphere of radius 5cm is immersed in water filled in a cylinder, the level of water rises 53cm. Find the radius of the cylinder.
View SolutionFind the number of sphere of radius r touching the coordinate axes.
View SolutionFind the number of sphere of radius r touching the coordinate axes.
View Solution
A cylinder whose base radius is 3 is inscribed in a sphere of radius 5. what is the difference between the volume of the sphere annd the volume of the cylinder?View SolutionA metallic solid sphere of radius 9 cm is melted to form a solid cylinder of radius 9 cm. Find the height of the cylinder.
View SolutionIn a hexagonal system system of crystals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are regular hexagons, and three atoms are sandwiched in between them. A space-cilling model of this structure, called hexagonal close-packed is constituted of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible. Three spheres are then placed overt the first layer so that they touch each other and represent the second layer so that they touch each other and present the second layer. Each one of the three spheres touches three spheres of the bottom layer. Finally, the second layer is converted with a third layer identical to the bottom layer in relative position. Assume the radius of every sphere to be r.
The number of atom in this hcp unit cell is
(a)4
(b)6
(c)12
(d)17View SolutionA cylinder is within the cube touching all the vertical faces. A cone is inside the cylinder. If their heights are same with the same base, find the ratio of their volumes.
View SolutionIn a hexaonal system system of cycstals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are refular hexagons, and three atoms are sandwiched in between them. A space-cilling model of this structure, called hexagonal close-paked is constituted of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible. Three spherres are then placed overt the first layer so that they toych each other and represent the second layer so that they toych each other and present the second layer. Each one of the three spheres touches three spheres of the bottom layer. Finally, the second layer is convered with a third layer identical to the bottom layer in relative position. Assume the radius of every sphere to be r.
The empty space in this hcp unit cell is
(a)74%
(b)48.6%
(c)32%
(d)26%View SolutionIn a hexaonal system system of cycstals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are refular hexagons, and three atoms are sandwiched in between them. A space-cilling model of this structure, called hexagonal close-paked is constituted of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible. Three spherres are then placed overt the first layer so that they toych each other and represent the second layer so that they toych each other and present the second layer. Each one of the three spheres touches three spheres of the bottom layer. Finally, the second layer is convered with a third layer identical to the bottom layer in relative position. Assume the radius of every sphere to be r.
The number of atom in this hcp unit cell isView Solution


