A rod of length 12 cm moves with its ends always touching the coordinate axes. Determine the equation of the locus of a point P on the rod, which is 3cm from the end in contact with the x-axis.
Let the AB lies on axes OX and OY. P(x,y) be a moving point at 3 cm distance from A.
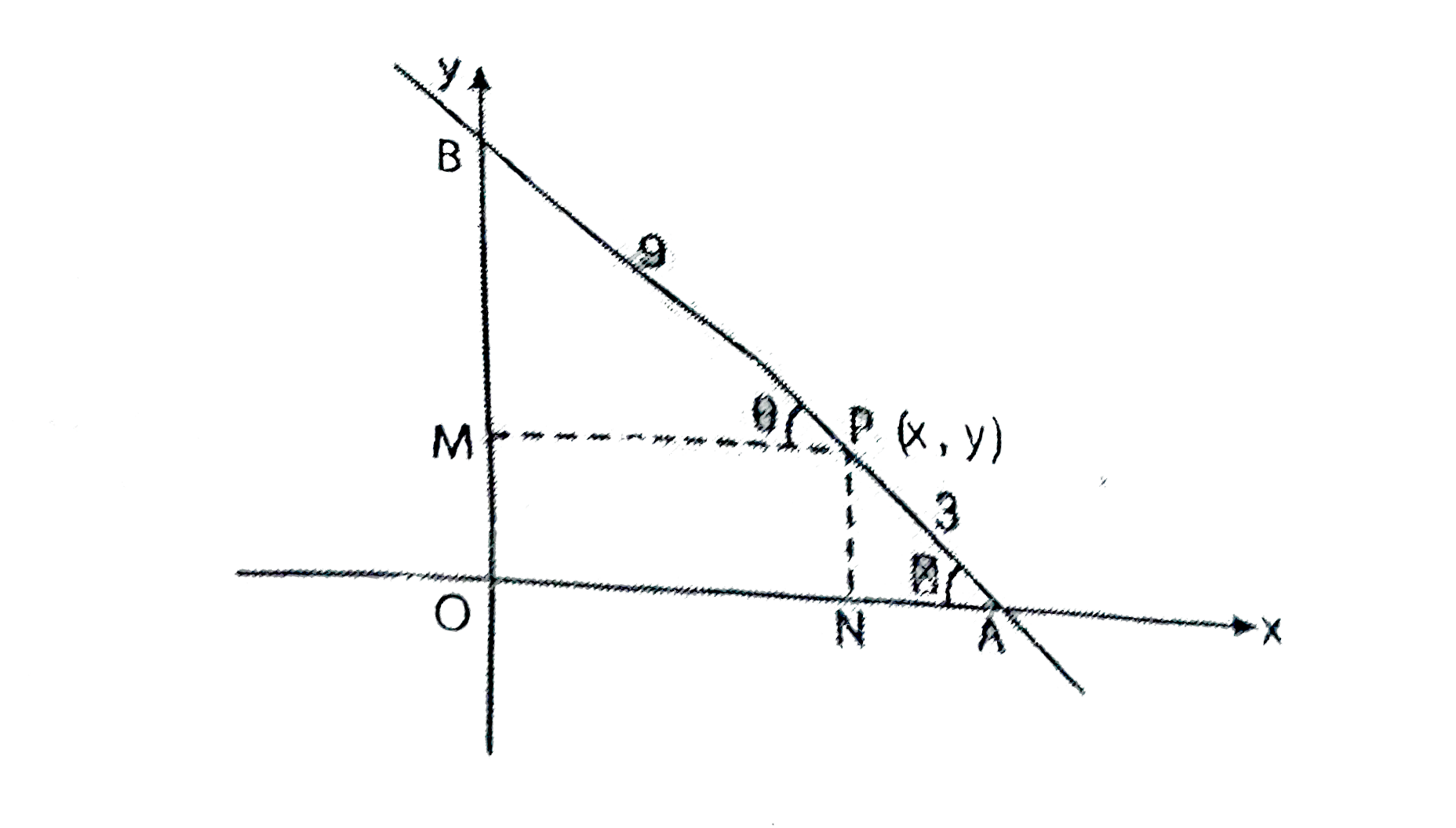
∴ BP=AB−AP=(12−3)cm=9cm
Let ∠(NAP)=∠(MPB)=θ
In ΔPMB, cosθ=x9
In ΔAPN, sinθ=y3
Now, from cos2θ+sin2θ=1
x281+y29=1 ⇒ x2+9y2=81
Topper's Solved these Questions
- CONIC SECTIONBook:NAGEEN PRAKASHAN ENGLISHChapter:CONIC SECTIONExercise:Exercise 11.4
Explore 15 Videos
- COMPLEX NUMBERS AND QUADRATIC EQUATION Book:NAGEEN PRAKASHAN ENGLISHChapter:COMPLEX NUMBERS AND QUADRATIC EQUATION Exercise:MISCELLANEOUS EXERCISE
Explore 20 Videos
- INTRODUCTION OF THREE DIMENSIONAL GEOMETRYBook:NAGEEN PRAKASHAN ENGLISHChapter:INTRODUCTION OF THREE DIMENSIONAL GEOMETRYExercise:Miscellaneous Exercise
Explore 6 Videos
Similar Questions
A rod AB of length 30 cm moves such that its ends always touching the co-ordinate axes. Determine the locus of a point C of the rod if AC : BC = 2 : 1
View SolutionA rod of length l cm moves with its ends A (on x=-axis) and B (on y-axis) always touching the coordinae axes. Prove that the point P on the rod which divides AB in the ratio λ(≠1) is ellipse. Alos, find the eccentricity of the ellipse.
View SolutionA rod AB of length 3 units moves vertically with its bottom B always an the circle x2+y2=25 then the equation of the locus of A is
View SolutionA straight rod of length 9 unit, slides with its ends A, B always on the x and y axes repectively. Then the locus of the centroid of ΔOAB is
View SolutionA rod of length k slides in a vertical plane, its ends touching the coordinate axes. Prove that the locus of the foot of the perpendicular from the origin to the rod is (x2+y2)3=k2x2y2.
View SolutionA rod of length k slides in a vertical plane, its ends touching the coordinate axes. Prove that the locus of the foot of the perpendicular from the origin to the rod is (x2+y2)3=k2x2y2.
View SolutionFind the equation of the locus of a point which moves so that its distance from the x-axis is double of its distance from the y-axis.
View SolutionA rod PQ of length 2a' slides with its ends on the axes then locus of circumference of triangle OPQ
View SolutionA rod AB of length 4 units moves horizontally with its left end A always on the circle x2+y2−4x−18y−29=0 then the locus of the other end B is
View SolutionA rod of length / slides with its ends on two perpendicular lines. Find the locus of its mid-point.
View Solution

