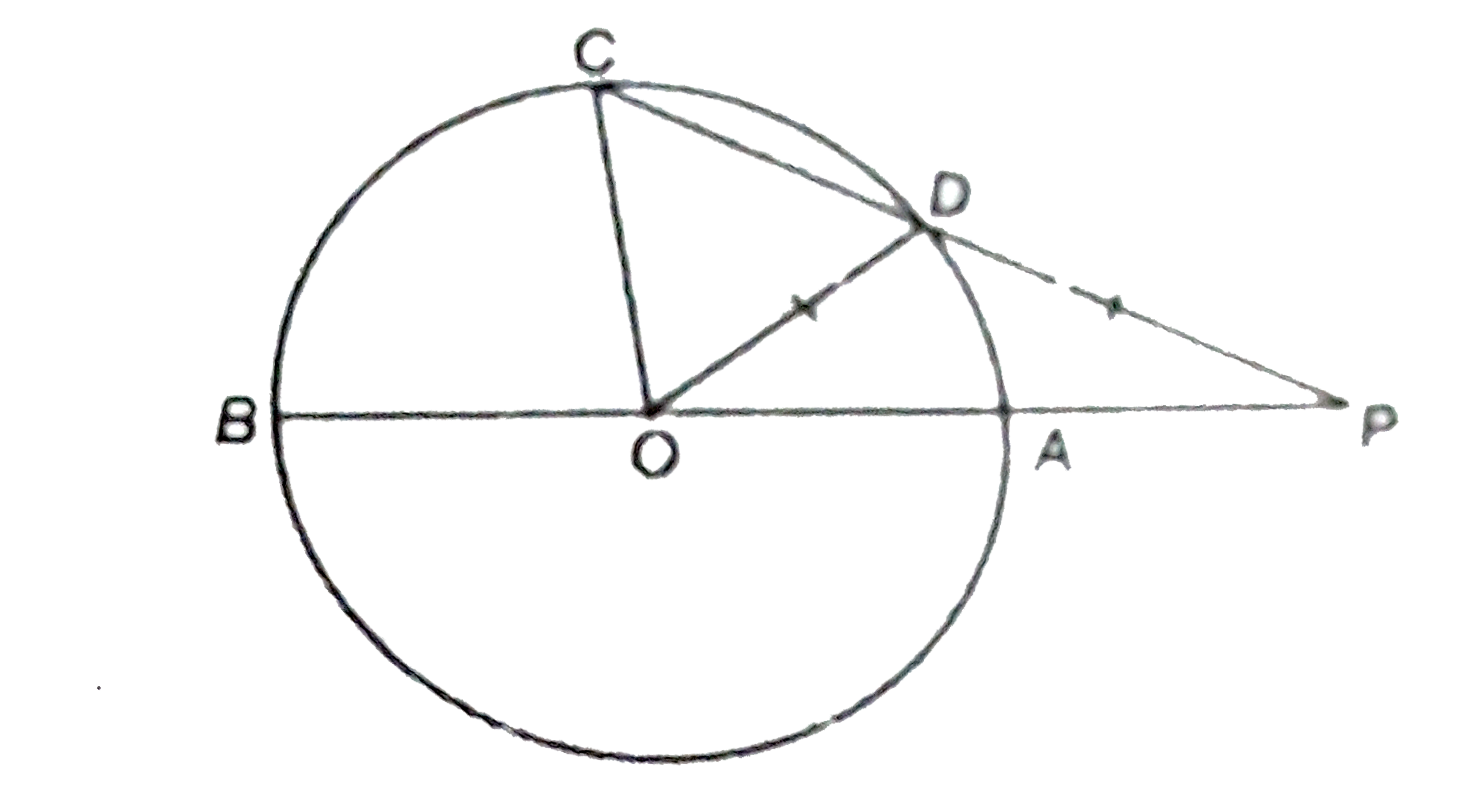
A point P lies outside the circle with centre O. two lines PAOB and PDC are drawn on the circle from P. if PD =OD, then prove that arc .
In ,
Let
Now in ,
is the exterior angle
In ,
Now, (L.P.A)
(length of arcs are proportional to their corresponding angles )
Topper's Solved these Questions
- CIRCLE Book:NAGEEN PRAKASHAN ENGLISHChapter:CIRCLE Exercise:Exercise 10a
Explore 22 Videos
- CIRCLE Book:NAGEEN PRAKASHAN ENGLISHChapter:CIRCLE Exercise:Exercise 10b
Explore 19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:AREA OF PARALLELOGRAMS AND TRIANGLESExercise:Revision Exercise (long Answer Question)
Explore 5 Videos
- CO-ORDINATE GEOMETRY Book:NAGEEN PRAKASHAN ENGLISHChapter:CO-ORDINATE GEOMETRY Exercise:Exercise
Explore 8 Videos
Similar Questions
From a point P outside a circle, with centre O, tangents PA and PB are drawn. Prove that
(i) ∠AOP=∠BOP
(ii) OP is the ⊥ bisector of chord AB.
View SolutionIf from an external point B of a circle with centre O, two tangents BC and BD are drawn such that ∠DBC=120∘, prove that BC+BD=BO.
View SolutionIn the following figure, P and Q are the points of intersection of two circles with centres O and O'. If straight lines APB and CQD are parallel to OO', prove that
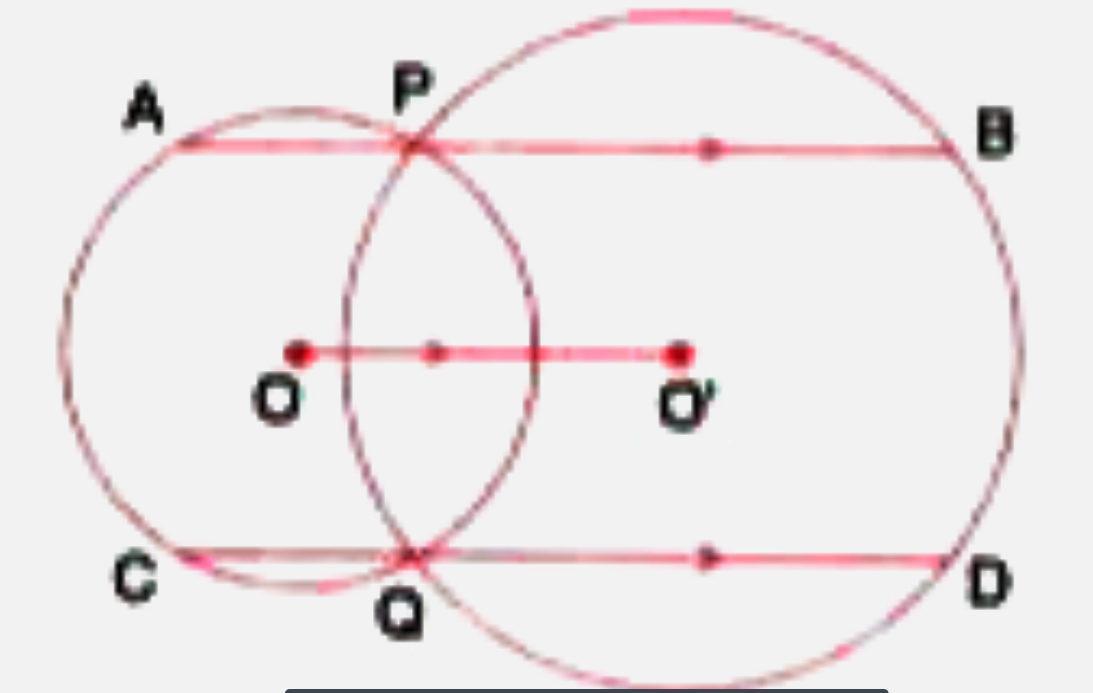
OO'=12AB=12CD
View SolutionIf from an extrenal point B of a circle with centre 0, two tangents BC and BD are drawn such that ∠DBC=120∘, prove that BC+BD=BO i.e., BO=2BC.
View SolutionIn the given figure, two tangents PQ and PR are drawn to a circle with centre O from an external point P, Prove that ∠QPR=2∠OQR.
View SolutionA point P is 13cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12 cm. Find the radius of the circle.
View SolutionDraw a circle of radius 3.5 cm. Take a point P outside the circle at a distance of 7 cm from the centre of the circle and construct a pair of tangents to the circle from the point.
View SolutionDraw a circle of radius 3.5 cm . Take a point P outside the circle at a distance of 7 cm from the centre of the circle and construct a pair of tangents to the circle from the point.
View SolutionIn the given figure, two tangents PQ and PR are drawn to a circle with centre C from an external point P, Prove that ∠QPR=2∠OQR.
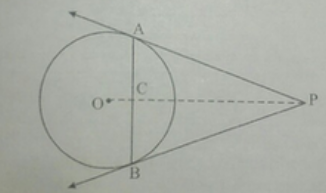
View SolutionFrom an external point P, two tangents PA and PB are drawn to the circle with centre O. Prove that OP is the perpendicular bisector of AB.
View Solution

