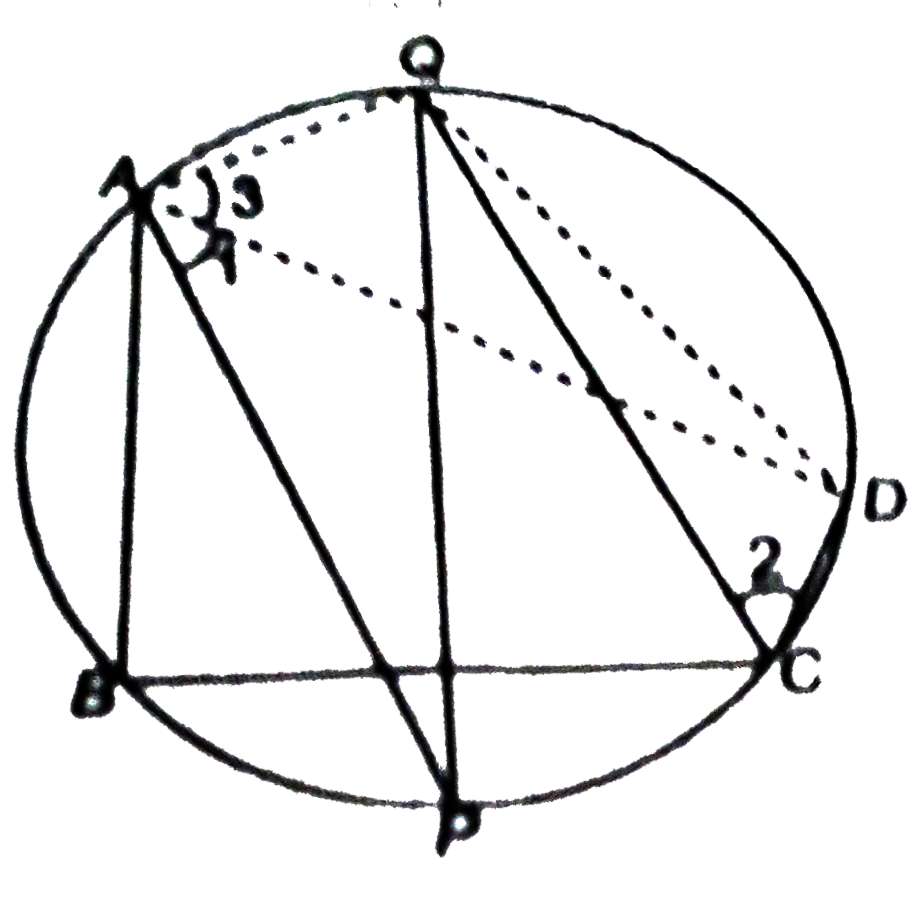
If bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.

Video Solution

Text Solution

Verified by Experts

The bisectors of opposite angles $∠ A$ and $∠ C$ of a cyclic qudarilateral ABCD intersect the circle at the point P and Q , respectively. We have to prove that PQ is a diameter of the circle.Join AQ and DQ. ltbr> Since, opposite angles of a cyclic quadrilateral are supplementary, so in cyclic qudarilateral ABCD, we have $∠ D A B + D C B = 180^{\circ}$
$∴ \frac{1}{2} ∠ D A B + \frac{1}{2} ∠ D C B = \frac{1}{2} (180^{\circ})$
$\Rightarrow ∠ 1 + ∠ 2 = 90^{\circ}$
$∴$ ( $∵ A P$ and $C Q$ are the bisectors of $∠ A$ and $a n l \geq C$ respectively).
$∠ 1 \to ∠ 3 = 90^{\circ} (∵ ∠ 2 = ∠ 3)$
( $∵ ∠ 2$ and $∠ 3$ are angles in the same segment of a circle with chord QD)
$\Rightarrow ∠ P A Q = 90^{\circ}$
$∴$ So, $a n l \geq P A Q$ is in a semi-circle.
Hence, PQ is a diameter of circle.

|

Updated on:21/07/2023

Class 9 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

NAGEEN PRAKASHAN ENGLISH-CIRCLE -Revision Exercise (long Answer Questions )

Home
Ask Doubt
Profile