Question

What must be added to $x^4+2x^3-2x^2+x-1$
so that the resulting polynomial is exactly
divisible by $x^2+2x-3.$

Explanation

Let `p(x)=x^(4)+2x^(3)-2x^(2)-2x-1`
and `g(x)=x^(2)+3x-3=(x-1)(x+3)`
`x^(2)+1`

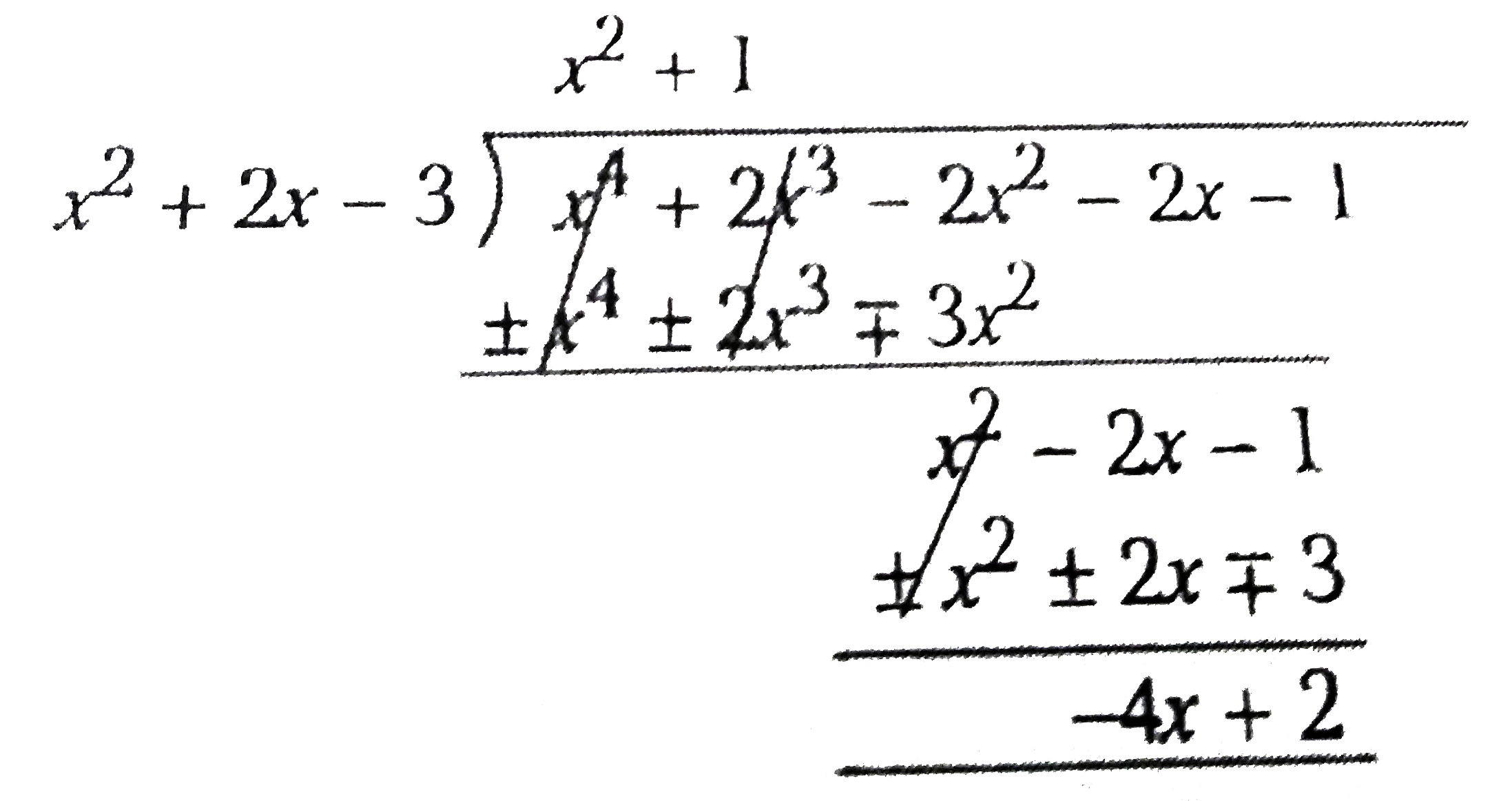
On actual division, we see that remainder (extra) is `-4x+2`. So, if we subtract `-4x+2` or add `-(-4x+2)` i.e., 4x-2 to p(x), then remainder vanishes, therefore p(x) will be exactly divisible by `x^(2)+2x-3`.
Hence, (4x-2) is added to the given polynomial p(x).
Alternative Method : Since p(x) is divided by a polynomial g(x) of degree 2, therefore we will get a remainder of degree 1.
Let (ax+b) be added to p(x) to get
`h(x)=(x^(4)+2x^(3)-2x^(2)-2x-a)+(ax+b)`
If equation (1) is divisible by `x^(2)+2x-3 " or" (x-1)(x+3)`
`therefore h(-3)=0` and h(1)=0
`implies (-3)^(4)+2(-3)^(3)-2(-3)^(2)-2(-3)-1+a(-3)+b=0`
`implies 81-54-18+6-1-3a+b=0 implies -3a +b=-14`
Also h(1)=0
`implies (1)^(4)+2(1)^(3)-2(1)^(2)-2(1)-1+a(1)+b=0`
`implies 1+2-2-2-1+a+b=0 implies a+b=2`
Subtracting (3) from (2), we get
`-4a=-16 implies a=4`
Put this value of a in (3), we get
b=-2
So, the required polynomial to be added =ax+b=4x-2.