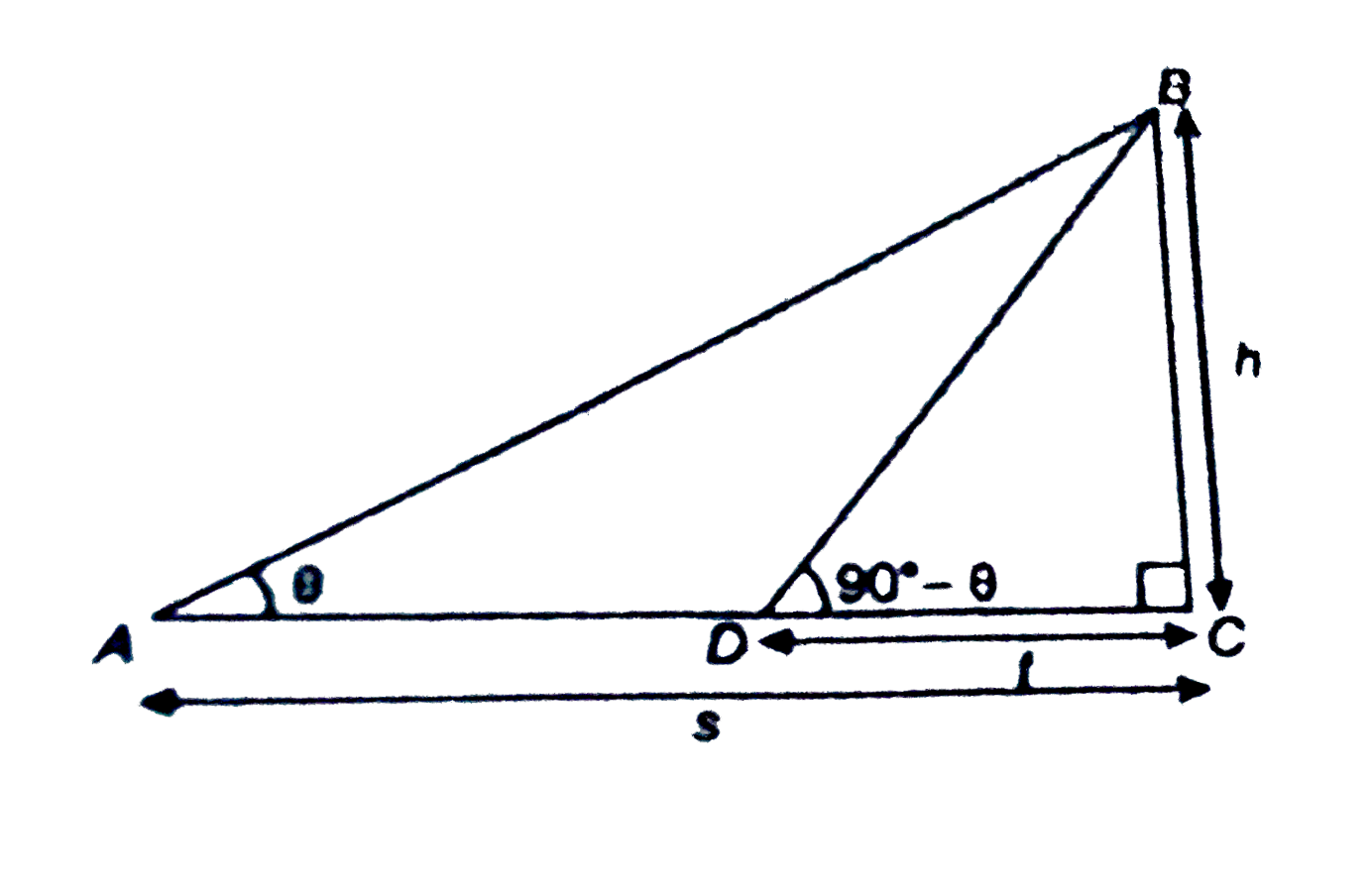
The angle of elevation of the top of a tower from two points distant s and t from its foot are complementary. Prove that the height of the tower is √st.
Let BC be a tower of height 'h'. Let AC=s and DC=t. From points A and D, the angle of elevation of top B of the tower are complementary.
Let ∠BAC=θ
∴∠BDC=90∘−θ
In ΔBAC
tanθ=BCAC=hs…(1)
In ΔBDC
tan(90∘−θ)=BCCD⇒cotθ=ht
⇒1tanθ=ht⇒sh=ht[om(1)]
⇒h2=st⇒h=√st
∴ height of the tower =√st
Topper's Solved these Questions
- SOME APPLICATIONS OF TRIGONOMETRYBook:NAGEEN PRAKASHAN ENGLISHChapter:SOME APPLICATIONS OF TRIGONOMETRYExercise:Exercise
Explore 32 Videos
- SOME APPLICATIONS OF TRIGONOMETRYBook:NAGEEN PRAKASHAN ENGLISHChapter:SOME APPLICATIONS OF TRIGONOMETRYExercise:Revision Exercise (short Answer Questions)
Explore 5 Videos
- REAL NUMBERSBook:NAGEEN PRAKASHAN ENGLISHChapter:REAL NUMBERSExercise:Revision Exercise Long Answer Questions
Explore 5 Videos
- STATISTICS Book:NAGEEN PRAKASHAN ENGLISHChapter:STATISTICS Exercise:Revision Exercise Long Answer Questions
Explore 4 Videos
Similar Questions
The angle of elevation of the top of a tower from two distinct points s and t from foot are complementary. Prove that the height of the tower is √st.
View SolutionIf the angles of elevation of a tower from two points distant a and b from the base and in the same straight line with it are complementary, then the height of the tower is
(a)ab
(b) √ab
(c) ab
(d) √ab
View SolutionThe angle of elevation of the top of a tower from a point 40 m away from its foot is 60∘. Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower at a point on the ground 50m away from the foot of the tower is 450. Then the height of the tower (in metres) is 50√3 (b) 50 (c) 50√2 (d) 50√3
View SolutionThe angles of elevation of the top of a tower from two points at a distances a meter and b metres from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is √ab metres.
View SolutionThe angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6m.
View SolutionThe angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
View SolutionThe angle of elevation of the top of a tower from a point on the ground is 60∘. which is 25 m away from the foot of the tower. Find the height of the tower
View SolutionThe angle of elevation of the top of a tower from a point on the ground, which is 30m away from the foot of the tower is 30∘ . Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower from a point on the ground, which is 30m away from the foot of the tower, is 30∘. Find the height of the tower.
View Solution