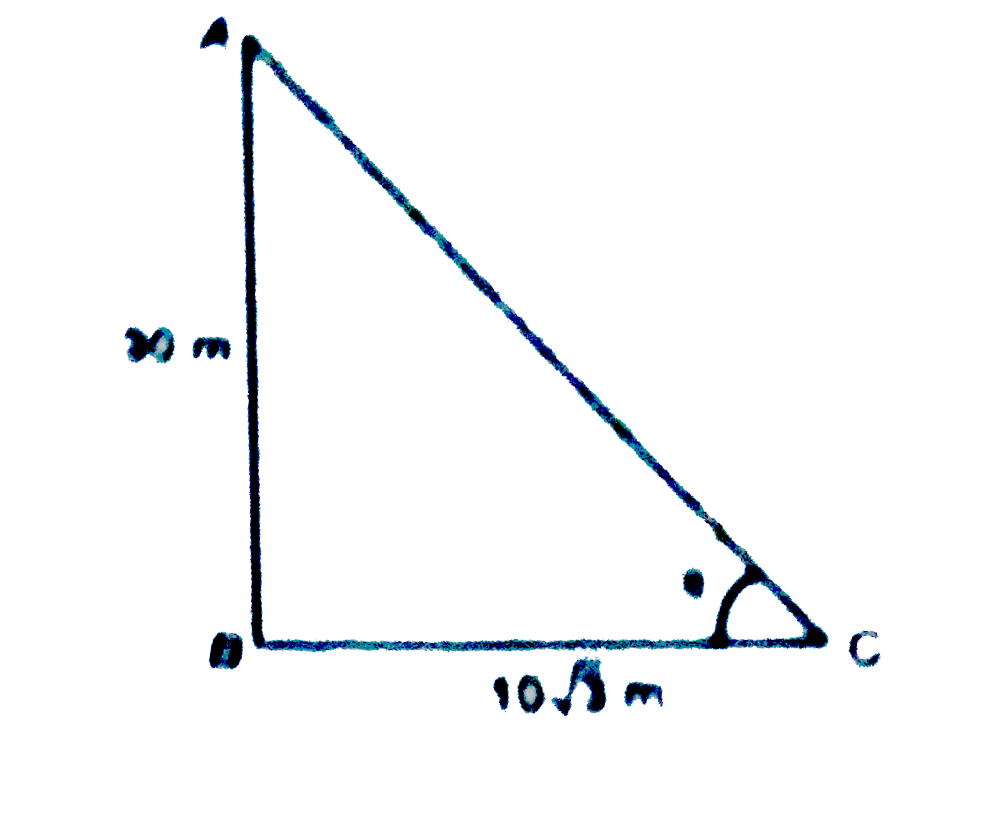
If a tower 30 m high, casts a shadow 10√3m long on the ground, then what is the angle of elevation of the sun ?
It is given that AB = 30 m be the tower and BC=10√3 m be its shadow on the ground.
Let θ be the angle of elevation.
In right triangle,
tanθ=ARBC
=3010√3=3√3=√3
=tan60∘
∴ θ=60∘
Hence, angle of elevation =60∘
Topper's Solved these Questions
- SOME APPLICATIONS OF TRIGONOMETRYBook:NAGEEN PRAKASHAN ENGLISHChapter:SOME APPLICATIONS OF TRIGONOMETRYExercise:Exercise
Explore 32 Videos
- SOME APPLICATIONS OF TRIGONOMETRYBook:NAGEEN PRAKASHAN ENGLISHChapter:SOME APPLICATIONS OF TRIGONOMETRYExercise:Revision Exercise (short Answer Questions)
Explore 5 Videos
- REAL NUMBERSBook:NAGEEN PRAKASHAN ENGLISHChapter:REAL NUMBERSExercise:Revision Exercise Long Answer Questions
Explore 5 Videos
- STATISTICS Book:NAGEEN PRAKASHAN ENGLISHChapter:STATISTICS Exercise:Revision Exercise Long Answer Questions
Explore 4 Videos
Similar Questions
If a tower 30 m high, casts a shadow 10√3m long on the ground, then what is the angle of elevation of the sun ?
View SolutionA pole 6 m high casts a shadow 2√3 m long on the ground, then find the angle of elevation of the sun.
View SolutionA pole of height 6 m casts a shadow 2√3 m long on the ground. Find the sun's elevation.
View SolutionIf a flag-staff of 6 m height placed on the top of a tower throws a shadow of 2√3 m along the ground, then what is the angle that the sun makes with the ground?
View SolutionIf a flag-staff of 6 m height placed on the top of a tower throws a shadow of 2√3 m along the ground, then what is the angle that the sun makes with the ground?
View SolutionIf the ratio of height of a tower and the length of its shadow on the ground is √3:1, then the angle of elevation of the sun is…………
View SolutionThe height of a tree is √3 times the length of its shadow. Find the angle of elevation of the sun
View SolutionA man is moving away from a tower 41.6 m high at the rate of 2 m/sec. Find the rate at which the angle of elevation of the top of tower is changing, when he is at a distance of 30m from the foot of the tower. Assume that the eye level of the man is 1.6m from the ground.
View SolutionA man is moving away from a tower 41.6 m high at the rate of 2 m/sec. Find the rate at which the angle of elevation of the top of tower is changing, when he is at a distance of 30m from the foot of the tower. Assume that the eye level of the man is 1.6m from the ground.
View SolutionA man is moving away from a tower 41.6 m high at the rate of 2 m/sec. Find the rate at which the angle of elevation of the top of tower is changing, when he is at a distance of 30m from the foot of the tower. Assume that the eye level of the man is 1.6m from the ground.
View Solution