Find the median of the following frequency distibution :
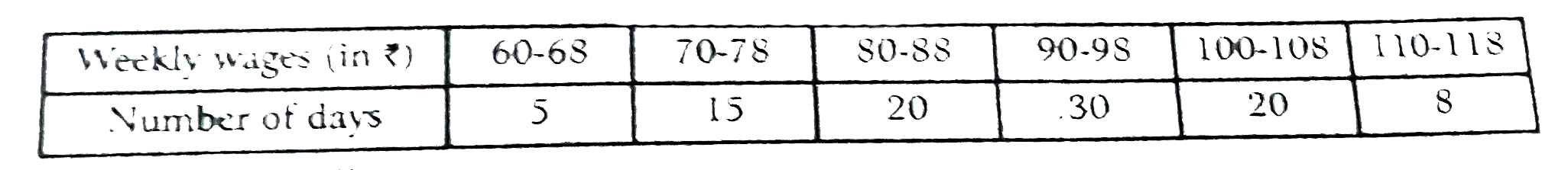
First of all we will prepare an exclusive series from the given (inclusive) series. To make it we subtract and add the same number, i.e.,70−682=1 in each class. So, new table is :

Here, N2=982=49
So, cumulative frequency just greater than or equal to 49 is 70 and its corresponding class is the medianl class.
∴ Median=l1+N2−Cf×i=89+49−4030×10+3=92
Topper's Solved these Questions
- STATISTICS Book:NAGEEN PRAKASHAN ENGLISHChapter:STATISTICS Exercise:Problems From NCERT/exemplar
Explore 4 Videos
- STATISTICS Book:NAGEEN PRAKASHAN ENGLISHChapter:STATISTICS Exercise:Exercise 14 A
Explore 17 Videos
- SOME APPLICATIONS OF TRIGONOMETRYBook:NAGEEN PRAKASHAN ENGLISHChapter:SOME APPLICATIONS OF TRIGONOMETRYExercise:Long Answer Questions
Explore 5 Videos
- TRIANGLES Book:NAGEEN PRAKASHAN ENGLISHChapter:TRIANGLES Exercise:Revision Exercise Long Questions
Explore 1 Video
Similar Questions
Find the median for the following frequency distribution:
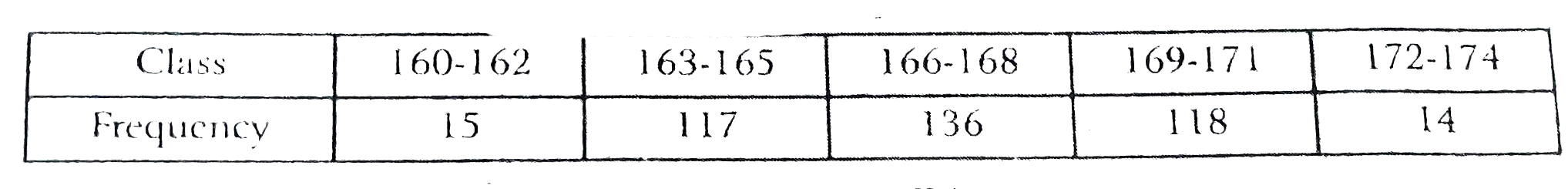
View SolutionFind the median of the following frequency distribution: Weekly wages (in Rs.) 60-69 70-79 80-89 90-99 100-109 110-119 No. of days: 5 15 20 30 20 8
View SolutionFind the median for the following frequency distribution :
Marks obtained(xi)293234274237Number of students(fi)25101284
View SolutionFind the mean for the following frequency distribution :
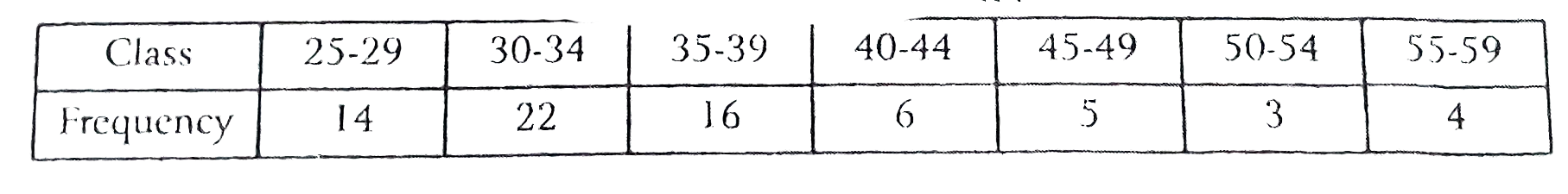
View SolutionFind the median from the following frequency distribution :
x34567891011f1390811176627622
View SolutionFind the mode of the following frequency distribution :
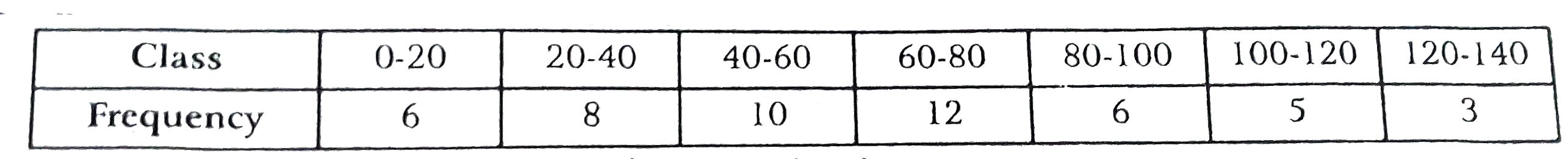
View SolutionFind the median from the following frequency distribution.
Number of students (f)1283214163Marks (x)40185010080160
View SolutionFind the mode of the following frequency distribution

View SolutionFind the mean of the following frequency distribution by direct method.

View SolutionCalculate the mean deviation about the median of the following frequency distribution: 5 7 9 11 13 15 17 Having Frequency 2 4 6 8 10 12 8
View Solution

