Two opposite vertices of a square are $(- 1, 2)$ and $(3, 2)$ . Find the coordinates of other two vertices.

Video Solution

Text Solution

Verified by Experts

Let PQRM be a square and let P(-1, 2) and R(3, 2) be the vertices.
Let the co-ordinates of Q be (x, y).
$∵ P Q = M R$
$\Rightarrow P Q^{2} = M R^{2}$
$\Rightarrow {(x + 1)}^{2} + {(y - 2)}^{2} = {(x - 3)}^{2} + {(y - 2)}^{2}$
$[∵ distance = \sqrt{{(x_{2} - x_{1})}_{2}^{2} + {(y_{2} - y_{1})}_{2}^{2}}]$

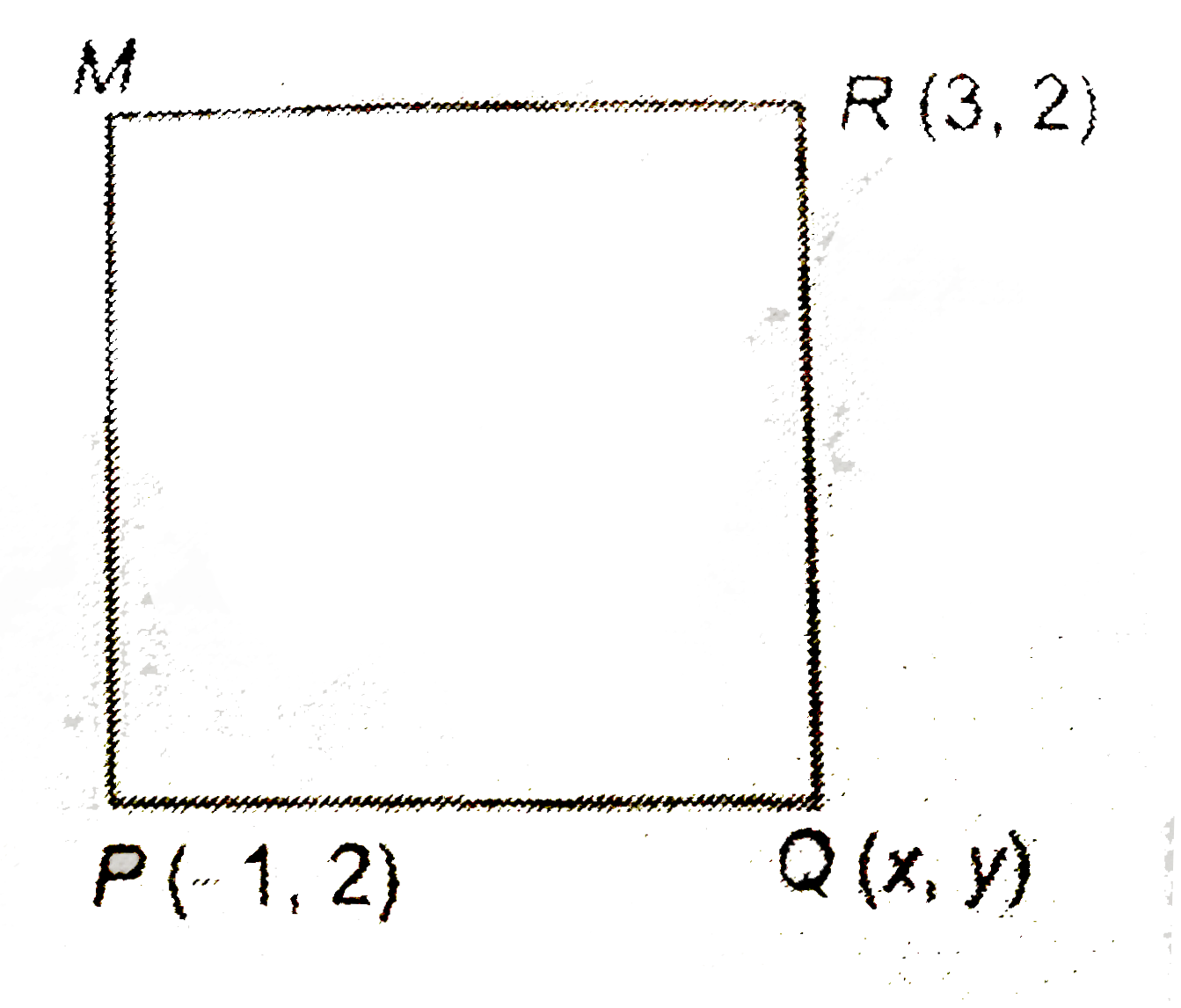
$\Rightarrow x^{2} + 1 + 2 x + y^{2} + 4 - 4 y = x^{2} + 9 - 6 x + y^{2} + 4 - 4 y$
$\Rightarrow 2 x + 1 = - 6 x + 9$
$\Rightarrow 8 x = 8 \Rightarrow x = 1$ ...(1)
In $Δ P Q R$ , we have
$P Q^{2} + Q R^{2} = P R^{2}$
${(x + 1)}^{2} + {(y - 2)}^{2} + {(x - 3)}^{2} + {(y - 2)}^{2} = {(3 + 1)}^{2} + {(2 - 2)}^{2}$
$\Rightarrow x^{2} + 1 + 2 x + y^{2} + 4 - 4 y + x^{2} + 9 - 6 x + y^{2} + 4 - 4 y = 4^{2} + 0^{2}$
$\Rightarrow 2 x^{2} + 2 y^{2} - 4 x - 8 y + 2 = 0$
$\Rightarrow x^{2} + y^{2} - 2 x - 4 y + 1 = 0 ... (2)$
Putting x=1 from eq. (1) in eq. (2), we get
$1 + y^{2} - 2 - 4 y + 1 = 0$
$\Rightarrow y^{2} - 4 y = 0$
$\Rightarrow y (y - 4) = 0 \Rightarrow y = 0 or 4$
Hence, the required vertices of square are (1, 0) and (1, 4).

|

Updated on:21/07/2023

Class 10 MATHS COORDINATE GEOMETRY

Topper's Solved these Questions

Similar Questions

NAGEEN PRAKASHAN ENGLISH-CO-ORDINATE GEOMETRY-Problems Of NCERT/exemplar

Home
Ask Doubt
Profile