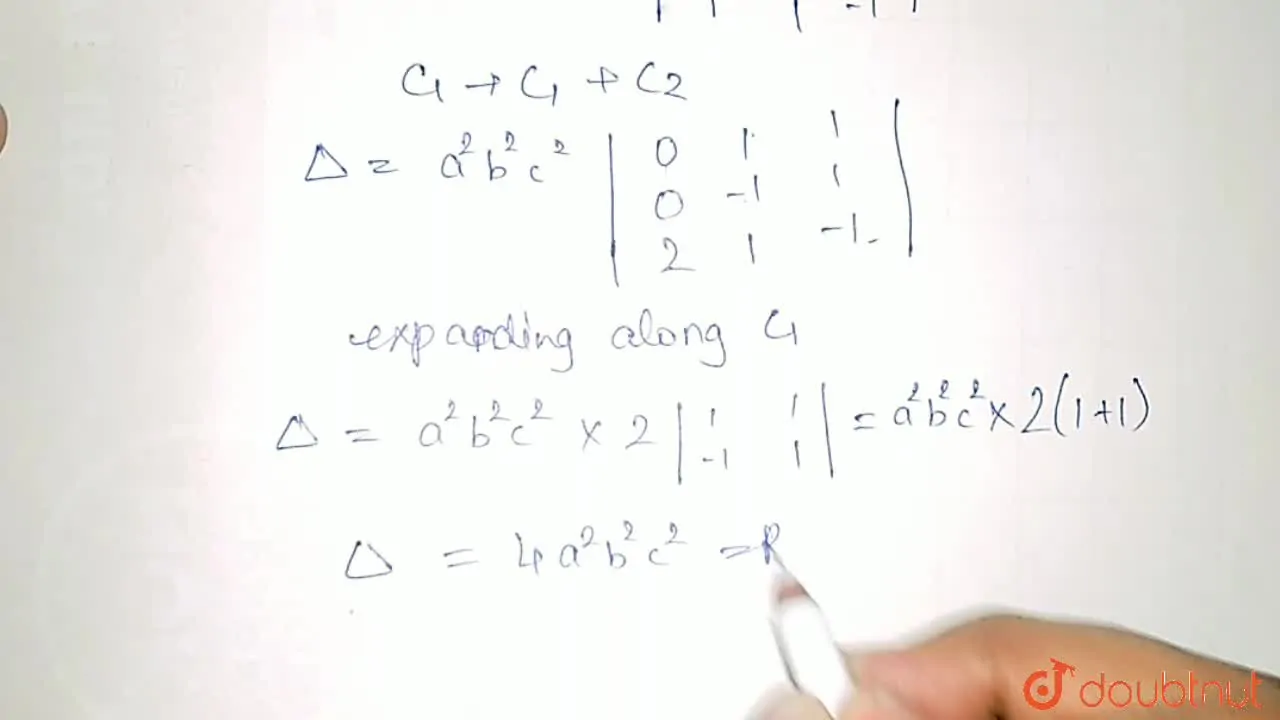Using the property of determinants and without expanding, prove that:∣∣−a2abacbab2bacb−c2∣∣=4a2b2c2
∣∣
∣
∣∣−a2abacba−b2accacb−c2∣∣
∣
∣∣=abc∣∣
∣∣−abca−bcab−c∣∣
∣∣
=a2b2c2∣∣
∣∣−111a−bcab−c∣∣
∣∣
=a2b2c2∣∣
∣∣−1110−1121−1∣∣
∣∣(C1→C1+C2)
=a2b2c2.2∣∣∣11−11∣∣∣
(Expanding along C1)
=a2b2c2(1+1)=4a2b2c2=R.H.S.
Related Playlists
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - DETERMINANTSEXERCISE - Exercise 4.35videos
DETERMINANTS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - DETERMINANTSEXERCISE - Exercise 4.45videos
DETERMINANTS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - DETERMINANTSEXERCISE - Exercise 4.18videos
DETERMINANTS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - Continuity and DifferentiabilityEXERCISE - Miscellaneous Exercise23videos
Continuity and Differentiability
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Miscellaneous Exercise18videos
DIFFERENTIAL EQUATIONS
Similar Questions
Using the property of determinants and without expanding, prove that:|0a−b−a0−cbc0|=0
View SolutionUsing the property of determinants and without expanding, prove that:∣∣ ∣ ∣∣−a2abacba−b2bccacb−c2∣∣ ∣ ∣∣=4a2b2c2
View SolutionUsing the property of determinants and without expanding, prove that:|1bca(b+c)1cab(c+a)1abx(a+b)|=0
View SolutionUsing the property of determinants and without expanding, prove that:∣∣ ∣ ∣∣xax+ayby+bzcz+c∣∣ ∣ ∣∣=0
View SolutionUsing the property of determinants and without expanding, prove that:∣∣ ∣∣0a−b−a0−cbc0∣∣ ∣∣=0
View SolutionUsing the property of determinants and without expanding, prove that:∣∣ ∣∣a−bb−cc−ab−cc−aa−bc−aa−bb−c∣∣ ∣∣=0
View SolutionUsing the property of determinants and without expanding, prove that:∣∣ ∣ ∣∣1bca(b+c)1cab(c+a)1abc(a+b)∣∣ ∣ ∣∣=0
View SolutionShow that: ∣∣b2+c2abacbac2+a2bccacba2+b2∣∣=4a2b2c2
View SolutionShow that: ∣∣b2+c2abacbac2+a2bacba2+b2∣∣=4a2 b2 c2 .
View SolutionUsing properties of determinants, prove that ∣∣ ∣ ∣∣a2bcac+c2a2+abb2acabb2+bcc2∣∣ ∣ ∣∣ = 4a2b2c2
View Solution