the restriction on n, k and p so that PY +Wywill be defined are :
K=3,p=n
K is arbitrary , p=2
p is arobitray , k-3
k=2,p=3
The correct Answer is:A
To determine the restrictions on n, k, and p such that PY+WY is defined, we need to analyze the orders of the matrices involved in the expression.
1. Identify the Orders of the Matrices:
- Let the orders of the matrices be defined as follows:
- P is of order p×k
- Y is of order 3×k
- W is of order n×3
2. Determine the Order of PY:
- The multiplication PY is defined if the number of columns in P is equal to the number of rows in Y.
- Therefore, for P of order p×k and Y of order 3×k:
- The condition for multiplication is k=3.
- The resulting order of PY will be p×k or p×3.
3. Determine the Order of WY:
- The multiplication WY is defined if the number of columns in W is equal to the number of rows in Y.
- Therefore, for W of order n×3 and Y of order 3×k:
- The condition for multiplication is 3=3 (which is always true).
- The resulting order of WY will be n×k or n×3.
4. Condition for Addition PY+WY:
- For the addition PY+WY to be defined, both matrices must have the same order.
- From the previous steps, we have:
- Order of PY is p×3
- Order of WY is n×3
- Therefore, we need:
- p=n
5. Summary of Conditions:
- From the analysis, we have two conditions:
- k=3
- p=n
Final Answer:
The restrictions on n, k, and p so that PY+WY will be defined are:
- k=3
- p=n
- Let the orders of the matrices be defined as follows:
- P is of order p×k
- Y is of order 3×k
- W is of order n×3
- The multiplication PY is defined if the number of columns in P is equal to the number of rows in Y.
- Therefore, for P of order p×k and Y of order 3×k:
- The condition for multiplication is k=3.
- The resulting order of PY will be p×k or p×3.
- The multiplication WY is defined if the number of columns in W is equal to the number of rows in Y.
- Therefore, for W of order n×3 and Y of order 3×k:
- The condition for multiplication is 3=3 (which is always true).
- The resulting order of WY will be n×k or n×3.
- For the addition PY+WY to be defined, both matrices must have the same order.
- From the previous steps, we have:
- Order of PY is p×3
- Order of WY is n×3
- Therefore, we need:
- p=n
- From the analysis, we have two conditions:
- k=3
- p=n
The restrictions on n, k, and p so that PY+WY will be defined are:
- k=3
- p=n
Topper's Solved these Questions
- MATRICESBook:NAGEEN PRAKASHAN ENGLISHChapter:MATRICESExercise:Exercise 3.3
Explore 12 Videos
- MATRICESBook:NAGEEN PRAKASHAN ENGLISHChapter:MATRICESExercise:Exercise 3.4
Explore 18 Videos
- MATRICESBook:NAGEEN PRAKASHAN ENGLISHChapter:MATRICESExercise:Exercise 3.1
Explore 10 Videos
- LINEAR PROGRAMMINGBook:NAGEEN PRAKASHAN ENGLISHChapter:LINEAR PROGRAMMINGExercise:Miscellaneous Exercise
Explore 9 Videos
- PROBABIILITYBook:NAGEEN PRAKASHAN ENGLISHChapter:PROBABIILITYExercise:Miscellaneous Exercise
Explore 19 Videos
Similar Questions
Assume X, Y, Z, W and P are matrices of order 2×n, 3×k, 2×p, n×3and p×k, respectively. Choose the correct answer
The restriction on n, k and p so that PY+WYwill be defined are:(A) k=3,p=n (B) k is arbitrary, p=2 (C) p is arbitrary, k=3 (D) k=2, p=3
View SolutionRestriction endonucleases are called so as they
View Solution
Knowledge Check
Let n(A) = 6 and n(B) = p . Then , the total number of non - empty relations that can be defined from A to B is
A6PBnP+1C6p−1D26p−1A student was asked to prove a statement P(n) by induction. He proved that P(k+1) is true whenever P(k) is true for all k≥5∈N and also that P(5) is true. On the basis of this he conclude that P(n) is true
(i) ∀n∈W
(ii) ∀n>5
(iii) ∀n≥5
(iv) ∀n<5A∀n∈WB∀n>5C∀n≥5D∀n<5
Let f be a relation on the set N of natural numbers defined by f={(n,3n):n∈N} is f a function from N → N . If so, find the range of f .
View SolutionIf N denotes the set of all positive integers and if f:N→N is defined by f(n)= the sum of positive divisors of n then f(2k⋅3), where k is a positive integer is
View SolutionAnalyze the action of restriction endonuclease in the given below diagram represented as P and Q .
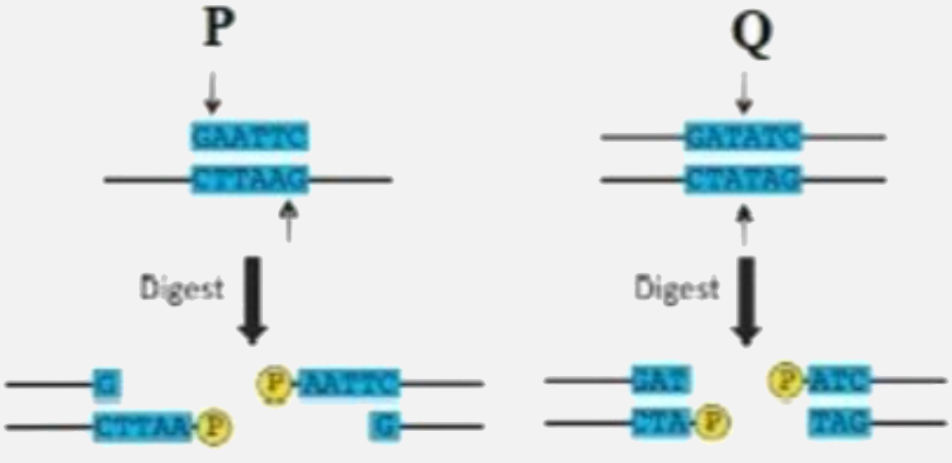
View SolutionLet O be the origin. We define a relation between two points P and Q in a plane if OP=OQ . Show that the relation, so defined is an equivalence relation.
View SolutionA be the set of two positive integers and f:A→Z+ (set of positive integer) defined as f(n)=p where p is the largest prime factor of n. If the range of f is {3}, find A.
View SolutionLet O be the origin. We define a relation between two points P and Q in a plane if OP=OQ. Show that the relation, so defined is an equivalence relation.
View Solution

