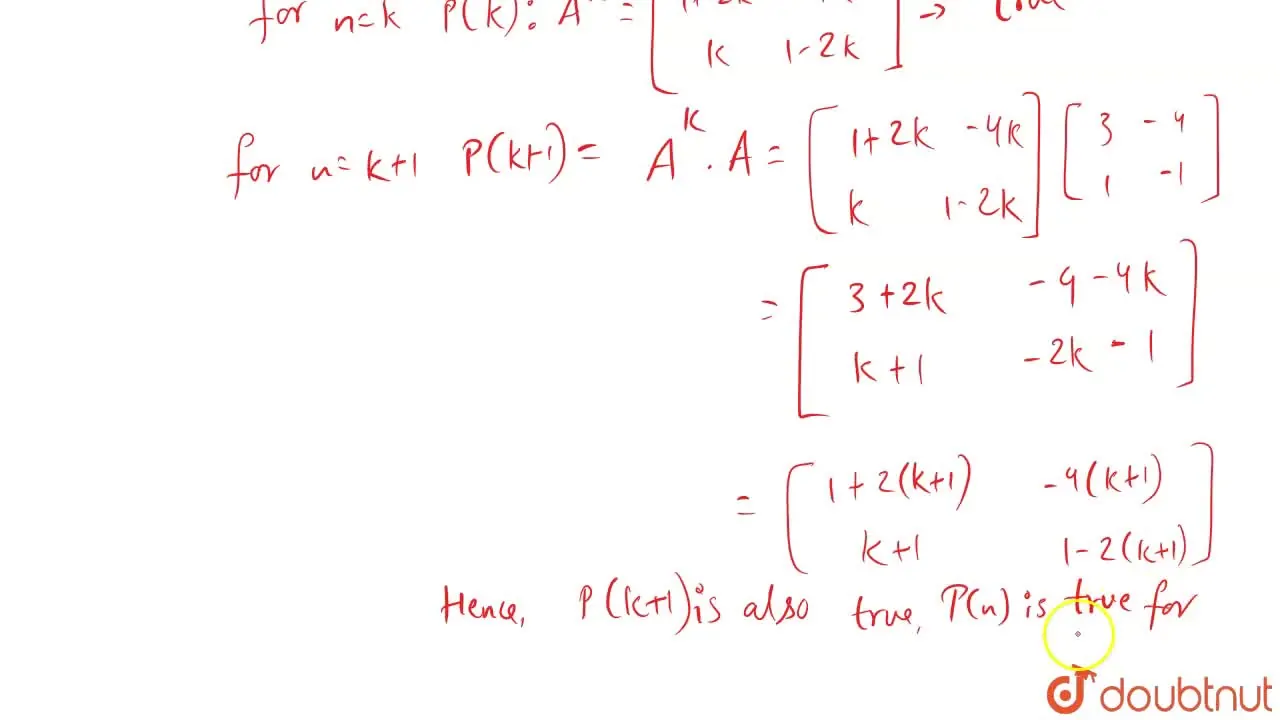ifA=[3−41m−1],then show that An=[1+2n−4nn1−2n] is true for all natural values of n.
Video Solution
Text Solution
The correct Answer is:N/a
N/a
|
Updated on:21/07/2023
Similar Questions
If A=[3−41−1] , then prove that An=[1+2n−4nn1−2n] , where n is any positive integer.
View SolutionIf A=[3−41−1], then prove that An=[1+2n−4nn1−2n], where n is any positive integer.
View SolutionShow that n3+(n+1)3+(n+2)3 is divisible by 9 for every natural number n.
View SolutionProve that1+2+22+...+2n=2n+1−1, for all natural number n.
View Solutionprove that 1+5+9+ . . .+(4n-3)=n(2n-1), for all natural number n.
View Solutionabout to only mathematics
View SolutionProve that 1n+1+1n+2+...+12n>1324 ,for all natural number n>1.
View SolutionIf 2n+1Pn−1:2n−1Pn=3:5, then find the value of n.
View SolutionProve the following by principle of mathematical induction If A=[3−41−1], then An=[1+2n−4nn1−2n] for every positive integer n
View SolutionIf A=[2−41−1] the value of An is (A) [3n(−4)n1(−1)n] (B) [3n−4nnn] (C) [2+n5−nn−n] (D) none of these
View Solution