Prove that the A.M. of two positive real numbers is greater than their G.M.
The correct Answer is:N/a
To prove that the Arithmetic Mean (A.M.) of two positive real numbers is greater than their Geometric Mean (G.M.), we will follow these steps:
Step 1: Define the two positive real numbers
Let the two positive real numbers be a and b.
Step 2: Calculate the Arithmetic Mean (A.M.)
The Arithmetic Mean of a and b is given by:
A.M.=a+b2
Step 3: Calculate the Geometric Mean (G.M.)
The Geometric Mean of a and b is given by:
G.M.=√ab
Step 4: Set up the inequality
We want to show that:
A.M.>G.M.
This translates to:
a+b2>√ab
Step 5: Rearranging the inequality
To eliminate the fraction, we can multiply both sides by 2 (since both a and b are positive, this does not change the direction of the inequality):
a+b>2√ab
Step 6: Square both sides
Next, we square both sides of the inequality to eliminate the square root:
(a+b)2>(2√ab)2
This simplifies to:
a2+2ab+b2>4ab
Step 7: Rearranging the terms
Now, we can rearrange the terms:
a2+b2+2ab−4ab>0
This simplifies to:
a2+b2−2ab>0
Step 8: Recognizing a perfect square
Notice that a2+b2−2ab can be rewritten as:
(a−b)2>0
Step 9: Conclusion
Since a and b are positive real numbers, (a−b)2 is always non-negative and is equal to zero only when a=b. Therefore, for a≠b, we have:
(a−b)2>0
This implies that:
A.M.>G.M.
Thus, we have proved that the Arithmetic Mean of two positive real numbers is greater than their Geometric Mean.
Let the two positive real numbers be a and b.
The Arithmetic Mean of a and b is given by:
A.M.=a+b2
The Geometric Mean of a and b is given by:
G.M.=√ab
We want to show that:
A.M.>G.M.
This translates to:
a+b2>√ab
To eliminate the fraction, we can multiply both sides by 2 (since both a and b are positive, this does not change the direction of the inequality):
a+b>2√ab
Next, we square both sides of the inequality to eliminate the square root:
(a+b)2>(2√ab)2
This simplifies to:
a2+2ab+b2>4ab
Now, we can rearrange the terms:
a2+b2+2ab−4ab>0
This simplifies to:
a2+b2−2ab>0
Notice that a2+b2−2ab can be rewritten as:
(a−b)2>0
Since a and b are positive real numbers, (a−b)2 is always non-negative and is equal to zero only when a=b. Therefore, for a≠b, we have:
(a−b)2>0
This implies that:
A.M.>G.M.
Thus, we have proved that the Arithmetic Mean of two positive real numbers is greater than their Geometric Mean.
Topper's Solved these Questions
- SEQUENCE AND SERIESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SEQUENCE AND SERIESEXERCISE - Exercise 9A
4 Videos
- SEQUENCE AND SERIESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SEQUENCE AND SERIESEXERCISE - Exercise 9B
18 Videos
- RELATIONS AND FUNCTIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - MISCELLANEOUS EXERCISE
12 Videos
- SETSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SETSEXERCISE - MISC Exercise
16 Videos
Similar Questions
Knowledge Check
If r and s are two positive numbers and r is 25% greater than s, what is the value of the ratio r/s?
A0.75B0.8C1D1.25The zeros of the polynomial function g are 4 and -2. If the range of g is the set real numbers greater than or equal to -3, which of the following could be the graph of y=g(x) in the xy-plane?
A B
B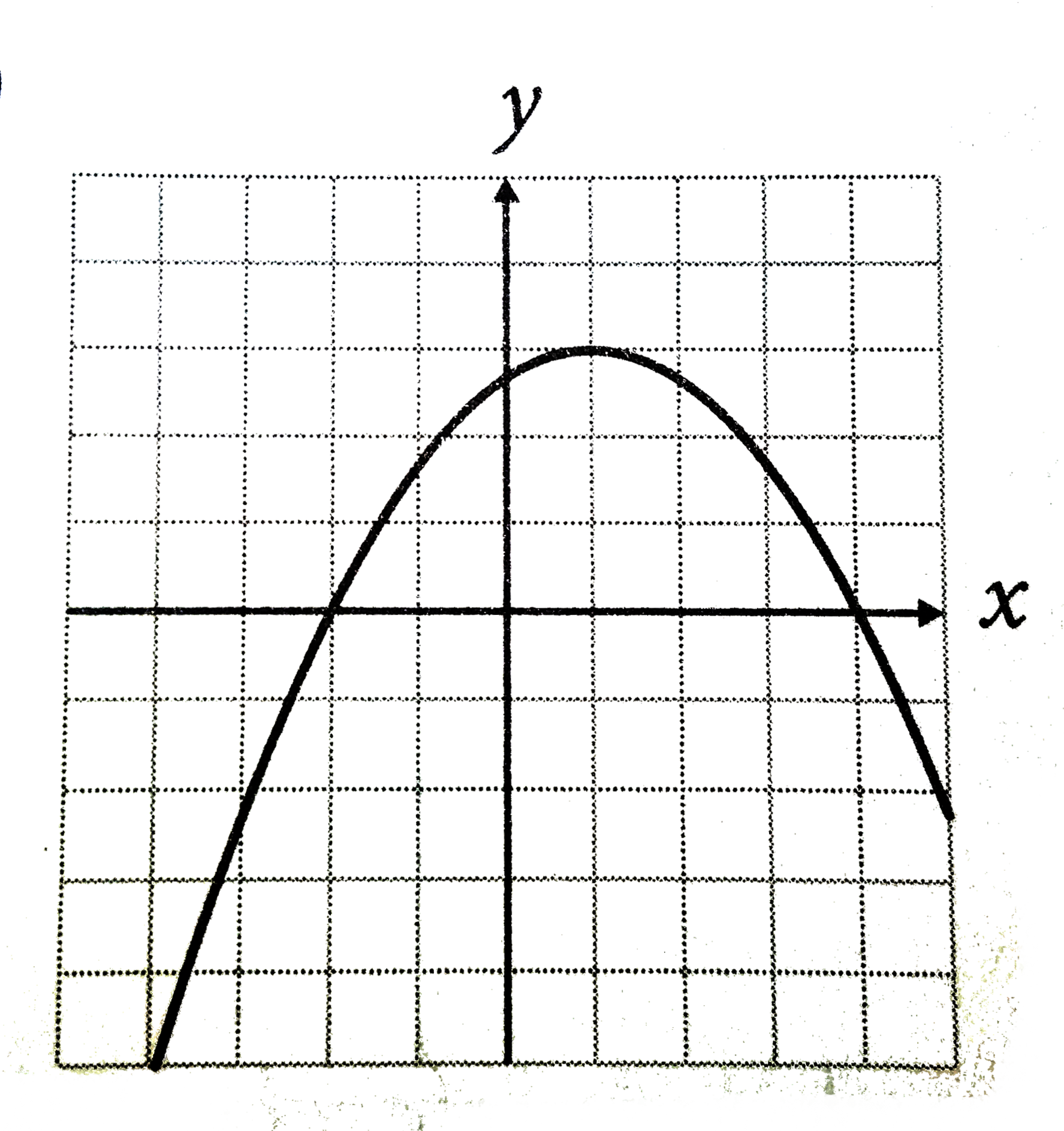 C
C D
D
If sum of the A.M.&G.M. of two positive distinct numbers is equal to the difference between the number then numbers are in ratio :
View SolutionIf the A.M. of two positive numbers aandb(a>b) is twice their geometric mean. Prove that : a:b=(2+√3):(2−√3).
View SolutionIf the A.M. of two positive numbers aandb(a>b) is twice their geometric mean. Prove that : a:b=(2+√3):(2−√3).
View SolutionIf the A.M. between two positive numbers exceeds their G.M. by 2 and the ratio of the numbers
be 1:4 find the numbers .
View SolutionThe A.M of two numbers is 17 and their G.M. is 8. Find the numbers.
View SolutionThe ratio of the A.M. and G.M. of two positive numbers a and b, is m : n. Show that a : b = (m+√m2−n2):(m−√m2−n2).
View Solution
