If one zero of a quadratic polynomial p(x)=ax2+bx+c is square of the other, then give the relation in a, b and c.
The correct Answer is:N/a
Let one zero of ax2+bx+c be α.
∴ other zero of ax2+bx+c be α2.
∴ sum of zeroes=α+α2=−ba ...(1)
and product of zeroes =α.α2=ca⇒α3=ca ......(2)
Now, from equation (1) since,
α+α2=−ba
∴ (α+α2)3=(−ba)3 (cubing both sides)
⇒α3+(α2)3+3α.α2(α+α2)=−b3a3 [using (a+b)3=a3+b3+3ab(a+b)]
⇒ α3+(α3)2+3α3(α+α2)=−b3a3
⇒ ca+(ca)2+3.ca(−ba)=−b3a3 [from (1) and (2)]
Multiplying both sides by a3
a2c+ac2−3abc=−b3
⇒ a2c+ac2+b3=3abc
This is the required relation. Ans.
Topper's Solved these Questions
- POLYNOMIALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - POLYNOMIALSEXERCISE - Problems From NCERT/ Exemplar
11 Videos
- POLYNOMIALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - POLYNOMIALSEXERCISE - Exercise 2a
28 Videos
- LINEAR EQUATIONS IN TWO VARIABLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - Revision Exercise Long Answer Questions
8 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABILITYEXERCISE - Revision Exercise Very Short Answer/short Answer Questions
16 Videos
Similar Questions
If one zero of the quadratic polynomial f(x)=4x2−8kx−9 is negative of the other, find the value of k .
View SolutionThe graph of quadratic polynomical f(x)=ax2+bx+c is shown below
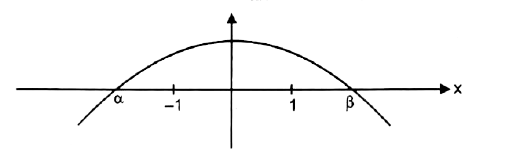
View SolutionIf one of the zeroes of a quadratic polynomial of the form x2+ax+b is the negative of the other, then it
View SolutionIf the zeroes of the quadratic polynomial x2+(a+1)x+b are 2 and -3, then: a and b are
View SolutionIf the squared difference of the zeros of the quadratic polynomial f(x)=x2+px+45 is equal to 144, find the value of p .
View SolutionIf one root of the equation ax2+bx+c=0 is double the other, then the relation between a,b,c is
View SolutionIf one root of the quadratic equation ax2+bx+c=0 is equal to the nth power of the other root , then show that (acn)1n+1+(anc)1n+1+b=0
View SolutionIf the zeroes of the quadratic ax2+bx+c where c≠0, are equal then:
View SolutionIf graph of the quadratic y=ax2+bx+c is given below :
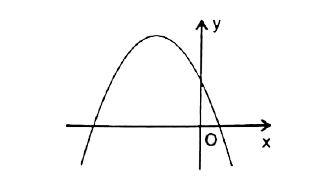 then:
then:
View SolutionIf a quadratic polynomial f(x) is a square of a linear polynomial, then its two zeroes are coincident. (True / False)
View Solution
