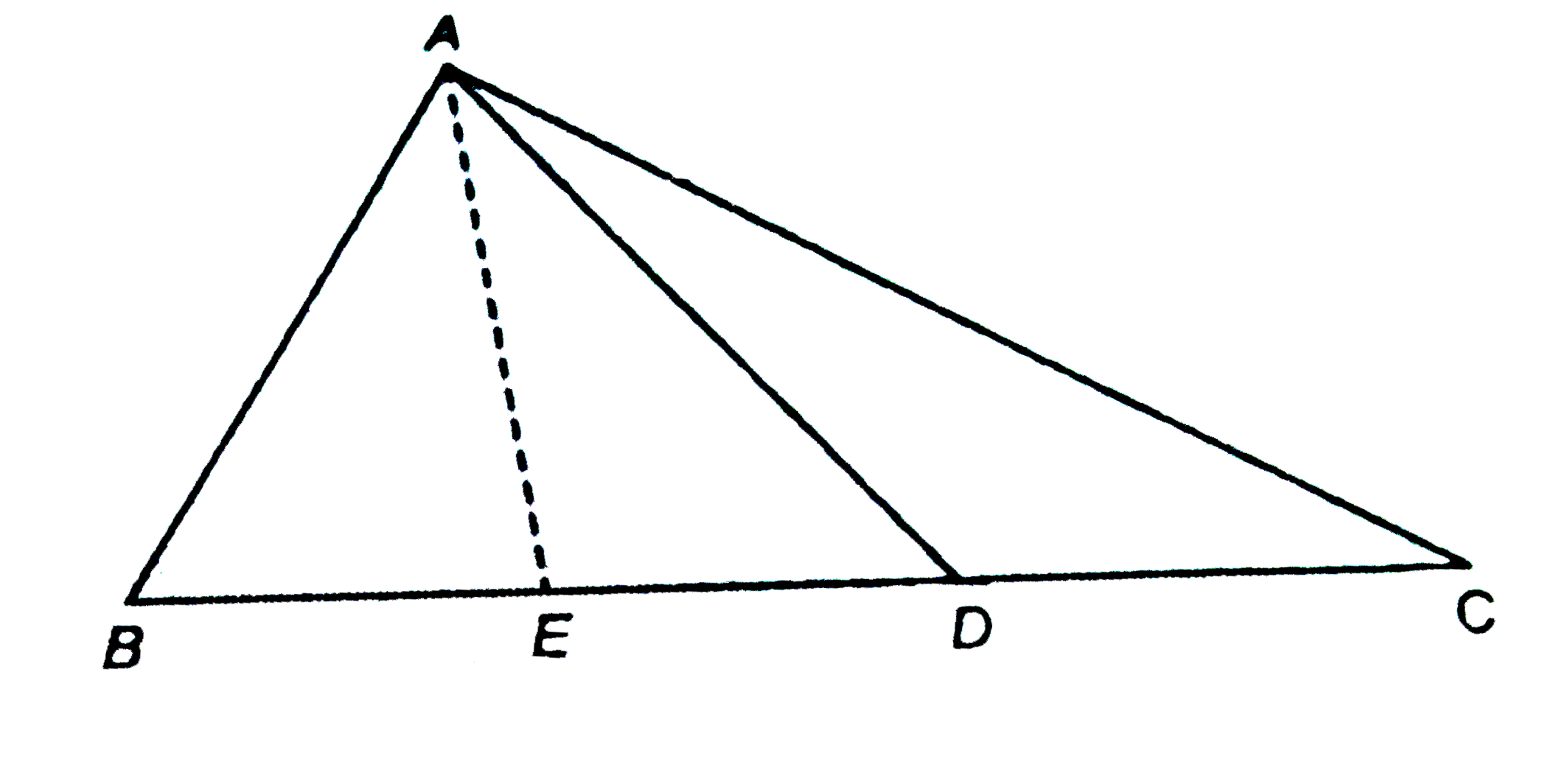
A point D is taken on the side BC of a ABC such that BD=2dC. Prove that ar(ABD)=2ar(ADC).
In ΔABC, we have BD=2DC
Let E is the mid-point of BD
Then, BE=ED=DC
Since, AE is the median of ΔABD
∴Ar(ΔABE)=ar(ΔAED)
(median divides the traingle into two equal areas) ...(1)
Also, since AD is the median of ΔAEC,
∴ar(ΔAED)=ar(ΔADC)
(median divides the triangle into two equal areas)...(2)
From eqs. (1) and (2), we have
ar(ΔABE)=ar(ΔAED)=ar(ΔADC)=x(say)
Now, ar(ΔABD)=ar(ΔABE)+ar(ΔAED)=x+x=2x=2×ar(ΔADC)
Topper's Solved these Questions
- AREA OF PARALLELOGRAMS AND TRIANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:AREA OF PARALLELOGRAMS AND TRIANGLESExercise:Problems From NCERT/exemplar
Explore 12 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:AREA OF PARALLELOGRAMS AND TRIANGLESExercise:Exercise
Explore 34 Videos
- CIRCLE Book:NAGEEN PRAKASHAN ENGLISHChapter:CIRCLE Exercise:Revision Exercise (long Answer Questions )
Explore 5 Videos
Similar Questions
A point D is taken on the side BC of a ABC such that BD=2DC. Prove that ar ( ABD)= 2 ar ( ADC)
View SolutionA point D is on the side BC of an equilateral triangle ABC such that DC=14 BC . Prove that AD2=13 CD2 .
View SolutionD is a point on the side BC of ABC such that ∠ADC=∠BAC . Prove that CACD=CBCA or, CA2=CB×CD .
View SolutionIn Figure D and E are two points on BC such that BD=DE=EC. Show that ar( ABD)= ar ( ADE)=ar ( AEC).
View SolutionIn Figure, AB=AC, D is the point in the interior of ABC such that ∠DBC= ∠DCB. Prove that AD bisects BAC of ABC.
View SolutionABCD is a parallelogram, G is the point on AB such that AG=2 GB, E is a point of DC such that CE=2DE and F is the point of BC such that BF=2FC. Prove that: ar (ADEG)= ar (GBCE)
View SolutionO is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(△OAB)=ar(△OBC)
View SolutionIn Figure, AB=AC and DB=DC. Prove that ∠ABD=∠ACD
View SolutionIn a ABC, If L and M are points on AB and AC respectively such that LM∣∣BC. Prove that: ar ( LBC)= ar ( MBC)
View SolutionAD is one of the medians of a ABC. X is any point on AD . Show that ar(ABX)=ar (ACX)
View Solution