In quadrilateral ABCD, diagonal BD is bisected by the diagonal AC. Prove that : ΔABCandΔADC are equal in area.
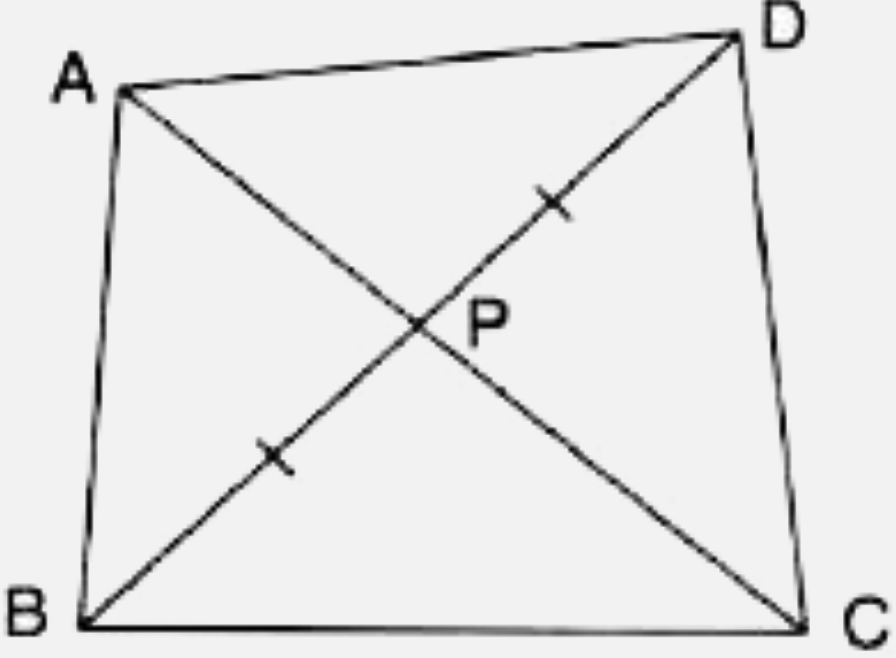
In □ABCD, the diagonals AC and BD intersect at 'O' such that
BO=OD
Now, in ∠ABD,O is the mid-point of BD
∴ are of ΔABO= area of ΔADO
(∴ median divides the triangle into two equal areas)...(1)
In ΔCBD,O is the mid-point of BD
∴ area of ΔCBO= area of ΔCDO
(∴ medians divides the triangle into two equal area)...(2)

Adding (1) and (2)
area of ΔABO+ area of ΔCBO= area of ΔADO+ area of ΔCDO
⇒ area of ΔABC= area of ΔADC
Topper's Solved these Questions
- AREA OF PARALLELOGRAMS AND TRIANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:AREA OF PARALLELOGRAMS AND TRIANGLESExercise:Problems From NCERT/exemplar
Explore 12 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:AREA OF PARALLELOGRAMS AND TRIANGLESExercise:Exercise
Explore 34 Videos
- CIRCLE Book:NAGEEN PRAKASHAN ENGLISHChapter:CIRCLE Exercise:Revision Exercise (long Answer Questions )
Explore 5 Videos
Similar Questions
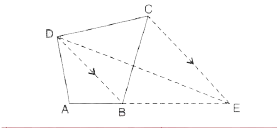
In the following figure, CE is drawn parallel to diagonal DB of the quadrilateral ABCD which meets AB produced ar point E.
Prove that ΔADE and quadrilateral ABCD are equal in area.
View SolutionIn a cyclic quadrilateral ABCD the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.
View SolutionIn trapezium ABCD, side AB is parallel to side DC. Diagonals AC and BD intersect at point P. Prove that triangles APD and BPC are equal in area.
View SolutionP is the mid-point of diagonal AC of quadrilateral ABCD. Prove that the quadrilaterals ABPD and CBPD are equal in area.
View SolutionIn quadrilateral ABCD, diagonals AC and BD intersect at point E such that
AE:EC=BE:ED.
Show that : ABCD is a trapezium.
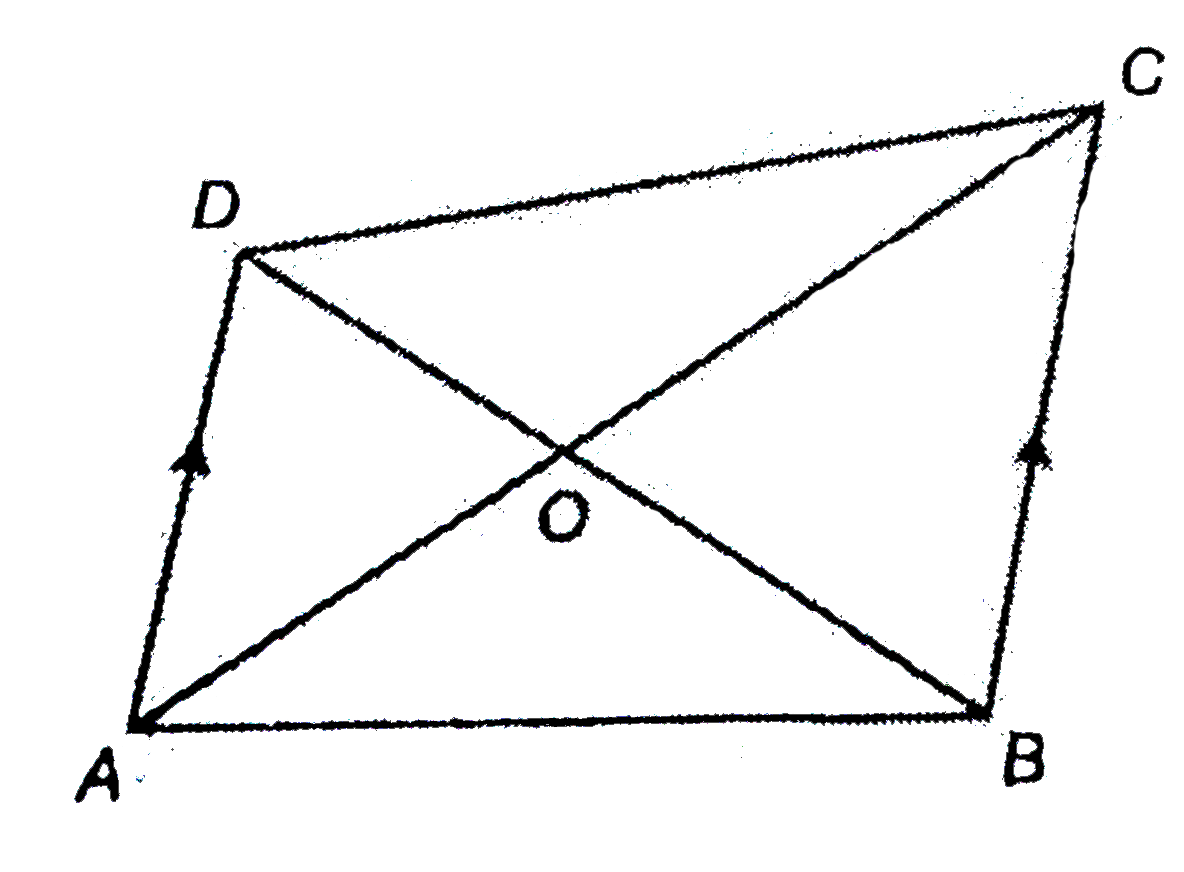
View SolutionIn the adjoining figure, ABCD is a quadrilateral in which AD∣∣BC. AC and BD intersect each other at point 'O'. Prove that:
area of ΔCOD= area of ΔABO
View SolutionA quadrilateral ABCD is such that diagonal BD divides its area in two equal parts. Prove that BD bisects AC GIVEN : A quadrilateral ABCD in which diagonal BD bisects it. i.e. ar(△ABD)=ar(△BDC) CONSTRUCTION : Join AC Suppose AC and BD intersect at O . Draw AL⊥BD. TO PROVE : AO=OC
View SolutionA quadrilateral ABCD is such that diagonal BD divides its area in two equal parts. Prove that BD bisects AC. GIVEN : A quadrilateral ABCD in which diagonal BD bisects it. i.e. ar(△ABD)=ar(△BDC) CONSTRUCTION : Join AC Suppose AC and BD intersect at O . Draw AM⊥BD and CN⊥BD. TO PROVE : AO=OC.
View SolutionProve that the diagonals of a rectangle bisect each other and are equal.
View SolutionThe diagonal AC of a quadrilateral ABCD divides it into two triangles of equal areas. Prove that diagonal AC bisects the diagonal BD.
View Solution