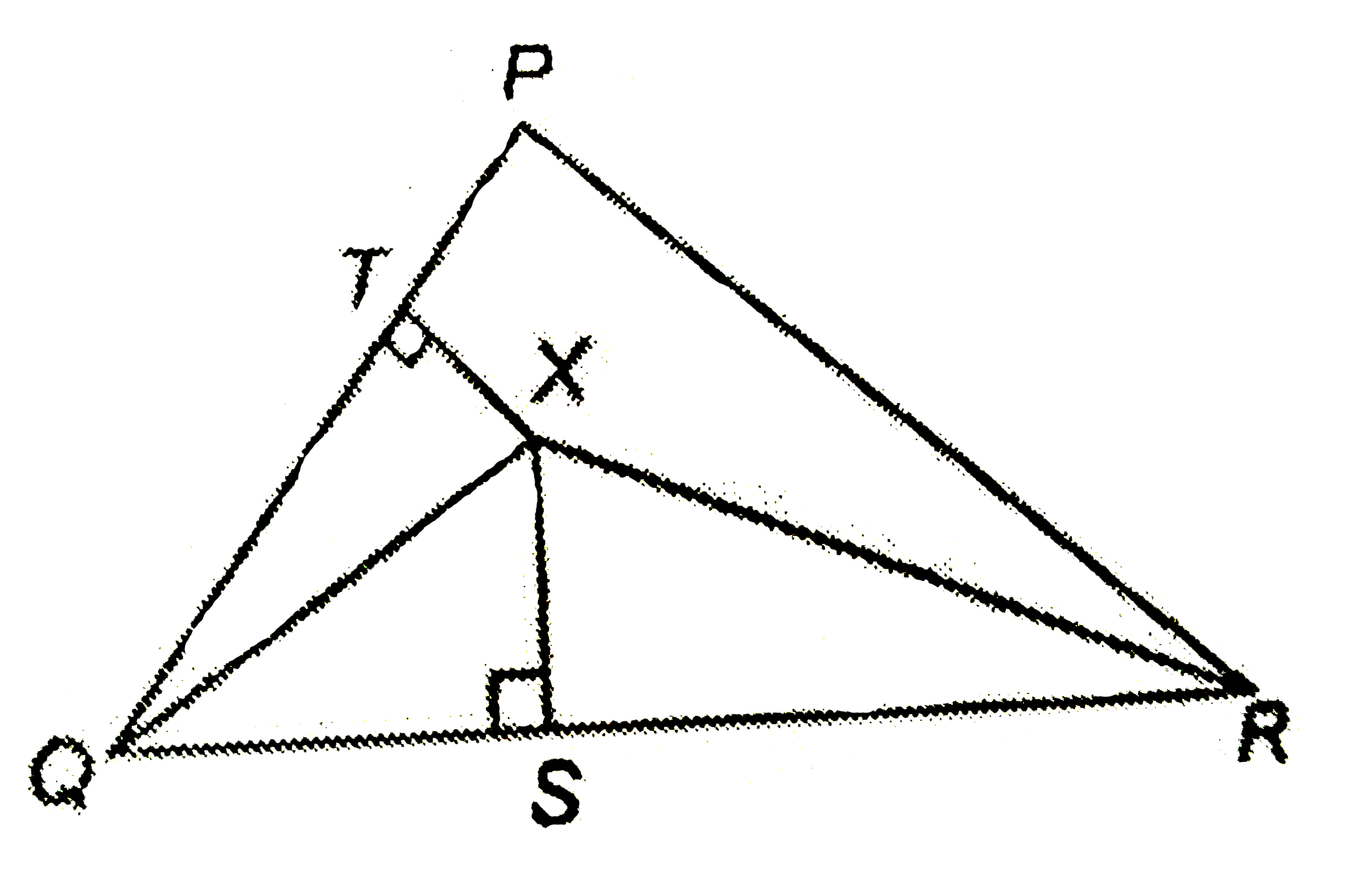
In the adjoining figure, QX and RX are the bisectors of the angles Q and R respectively of the angles Q and R respectively of the triangle PQR. If XS⊥PQ. Prove that :
(i) ΔXTQ≅ΔXSQ
(ii) PX bisects angle P.
Step by step video & image solution for In the adjoining figure, QX and RX are the bisectors of the angles Q and R respectively of the angles Q and R respectively of the triangle PQR. If XS bot PQ. Prove that : (i) DeltaXTQ cong DeltaXSQ (ii) PX bisects angle P. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:TRIANGLESExercise:Exercise 7b
Explore 17 Videos
- TRIANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:TRIANGLESExercise:Revision Exercise (very Short Answer Questions)
Explore 10 Videos
- TRIANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:TRIANGLESExercise:Problems From NCERT/exemplar
Explore 5 Videos
- SURFACE AREA AND VOLUMEBook:NAGEEN PRAKASHAN ENGLISHChapter:SURFACE AREA AND VOLUMEExercise:Revision Exercise (long Answer Questions)
Explore 10 Videos
Similar Questions
In the adjoining figure, OX and RX are the bisectors of the angle Q and R respectively of the triangle PQR. If XS⊥QR and XT⊥PQ.
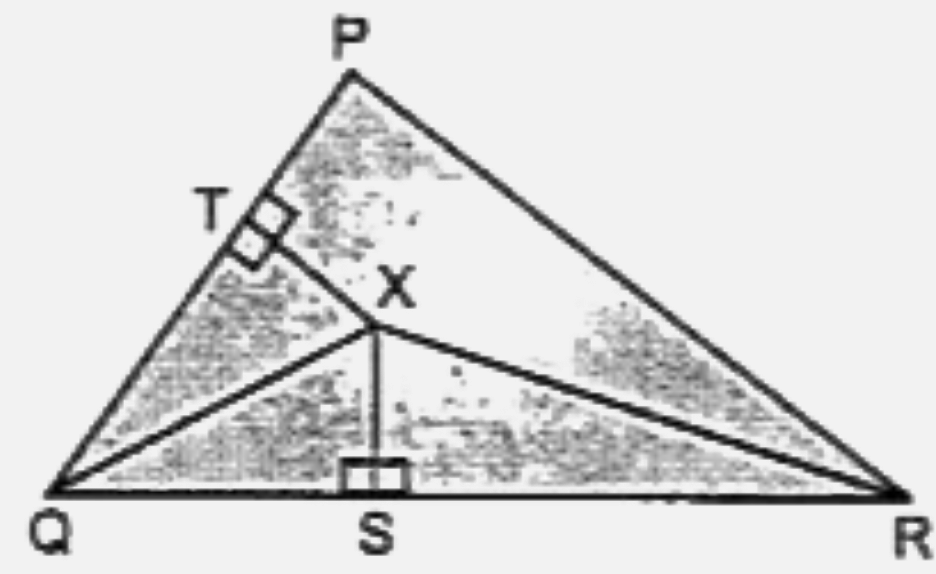
Prove that :
ΔXTQ≅ΔXSQ
View SolutionIn the adjoining figure, OX and RX are the bisectors of the angle Q and R respectively of the triangle PQR. If XS⊥QR and XT⊥PQ.
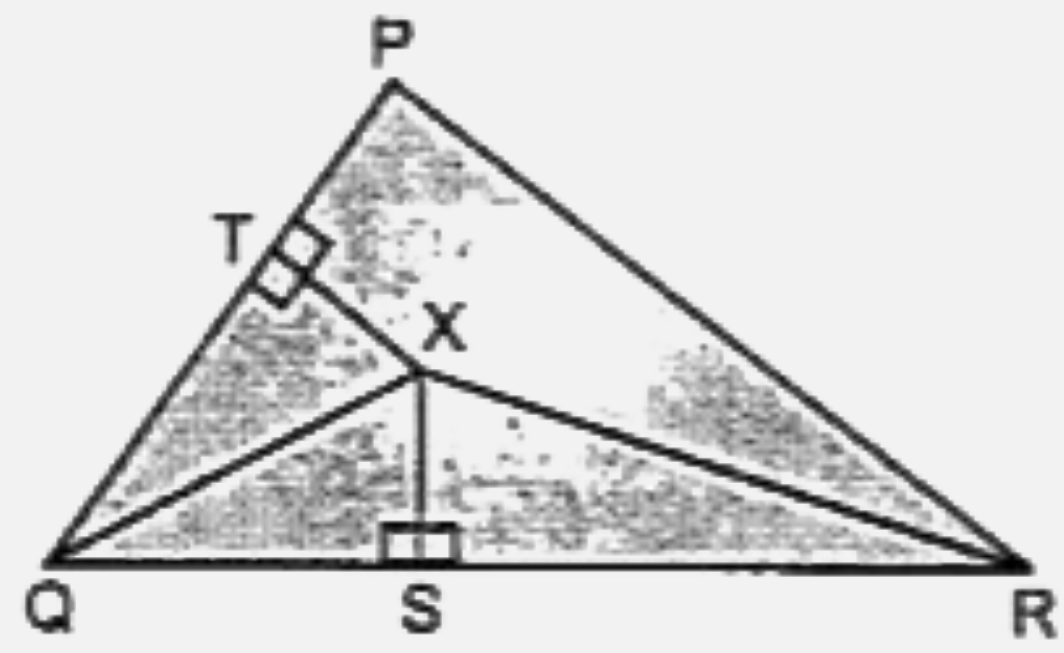
Prove that :
PX bisects angle P.
View SolutionIn the adjoining figure, QX and RX are the bisectors of the angles Q and R respectively of the triangle PQR.
If XS⊥QRandXT⊥PQ, prove that :
ΔXTQ≅ΔXSQ
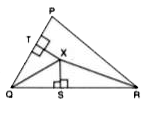
View SolutionIn Figure, PQ>PR.QS and RS are the bisectors of ∠Q and ∠R respectively. Prove that SQ>SR.
View SolutionIn the given triangle P, Q and R are the mid points of sides AB, BC and AC respectively. Prove that triangle PQR is similar to triangle ABC.

View SolutionIn the adjoining figure, AB>AC and the angle bisectors of ∠B and ∠C meet at point P. Prove that
PB>PC.

View SolutionIn the given PR is the bisector of ∠BPC.It meets BC and AD at points Q and R respectively. Prove that:
∠ARQ=∠BQR
View SolutionIn the given PR is the bisector of ∠BPC.It meets BC and AD at points Q and R respectively. Prove that:

angle ARQ + angle RQC = 180^(@)
View SolutionIn the adjoining figure, p||q. Find the unknown angles.
View SolutionIf p , q , r are the legths of the internal bisectors of angles A ,B , C respectively of a !ABC , then area of ABC

View Solution

