In right triangle ABC, right angle at C, M is the mid-point of the hydrotenuse AB. C is joined to M and produced to a point D such that DM=CM. Point D is joined to point B. Show that
(i) ΔAMC≅ΔBMD (ii) ∠DBC=∠ACB
(iii) ΔDBC≅ΔACB (iv) CM=12AB
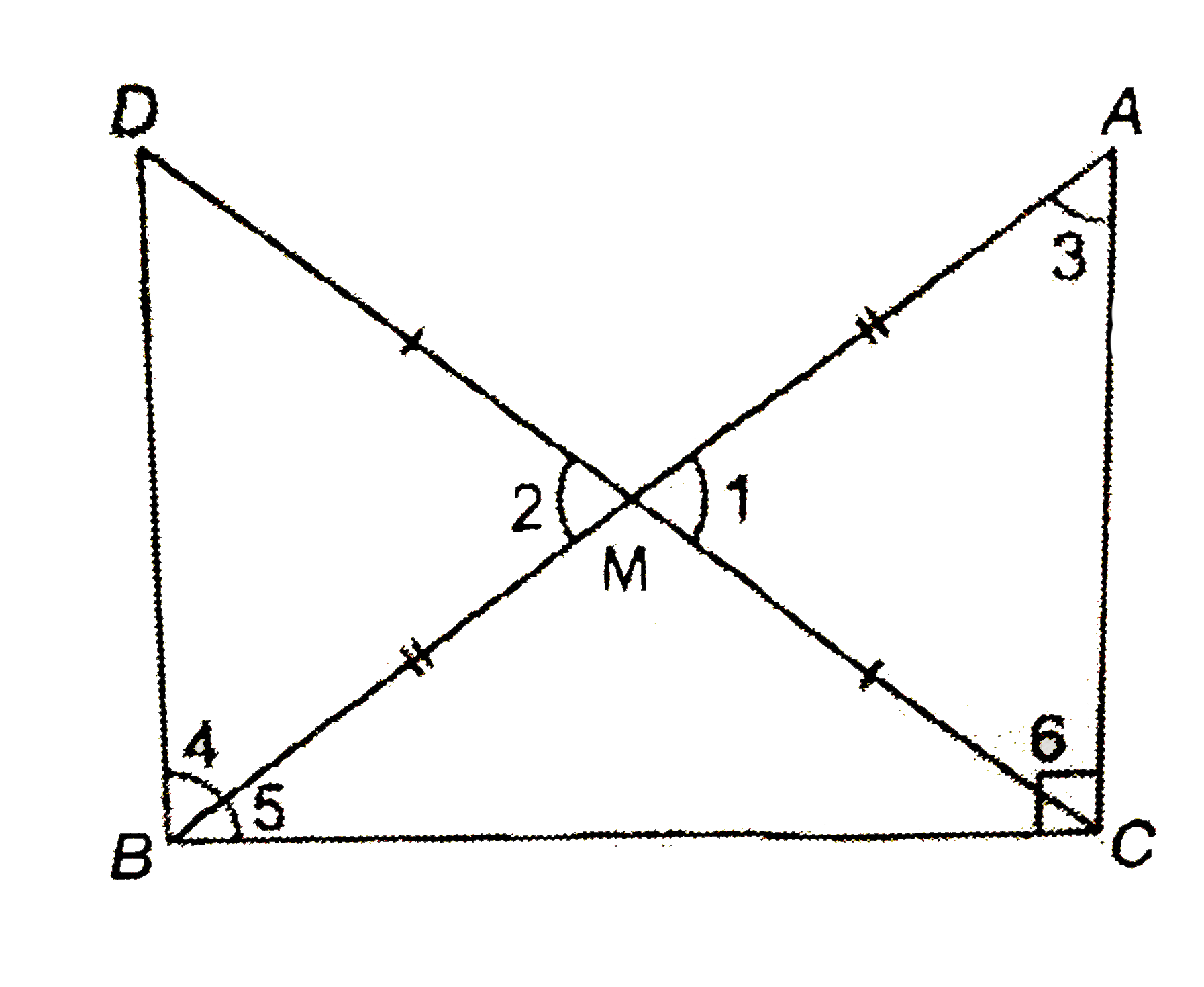
(i) In ΔAMC and ΔBMD,
∵⎧⎪⎨⎪⎩AM=BM(∵ M is the mid-point)∠1=∠2(vertically opposite angles)CM=DM(given)
∴ΔAMC≅ΔBMD (SAS)
⇒ AC=DB (c.p.c.t) ...(1) Hence Proved.
(ii) ∴∠3=∠4 (c.p.c.t.)
But these are the alternate angles which are equal.
∴AC∣∣BD
∴(∠4+∠5)+∠6=180∘ (sum of co-int ∠5 angles)
⇒ ∠4+∠5=180∘−90∘ (∵∠6=90∘, given)
⇒ ∠4+∠5=90∘
⇒ ∠DBC=90∘=∠ACB Hence Proved.
(iii) In ΔDBC and ΔACB,
∵⎧⎪⎨⎪⎩DB=AC[from (1)]∠DBC=∠ACB(just proved)BC=BC(common)
∴ΔDBC≅ΔACB (ASA) Hence Proved.
(iv) DC=AB (c.p.c.t)
⇒ 2CM=AB (∵ M is the mid-point of DC)
⇒ CM=12AB. Hence Proved.
Topper's Solved these Questions
- TRIANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:TRIANGLESExercise:Problems From NCERT/exemplar
Explore 5 Videos
- TRIANGLESBook:NAGEEN PRAKASHAN ENGLISHChapter:TRIANGLESExercise:Exercise 7a
Explore 35 Videos
- SURFACE AREA AND VOLUMEBook:NAGEEN PRAKASHAN ENGLISHChapter:SURFACE AREA AND VOLUMEExercise:Revision Exercise (long Answer Questions)
Explore 10 Videos
Similar Questions
In a right triangle ABC, right angled at C, P is the mid-point of hypotenuse AB. C is joined to P and produced to a point D, such that DP = CP. Point D is joined to point B. Show that:
ΔAPC≅ΔBPD
View SolutionIn a right triangle ABC, right angled at C, P is the mid-point of hypotenuse AB. C is joined to P and produced to a point D, such that DP = CP. Point D is joined to point B. Show that:
CP=12AB
View SolutionIn a right triangle ABC, right angled at C, P is the mid-point of hypotenuse AB. C is joined to P and produced to a point D, such that DP = CP. Point D is joined to point B. Show that:
ΔDBC≅ΔACB
View SolutionIn a right triangle ABC, right angled at C, P is the mid-point of hypotenuse AB. C is joined to P and produced to a point D, such that DP = CP. Point D is joined to point B. Show that:
Angle DBC is a right angle.
View SolutionIn right triangle ABC, right-angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see Fig. 7.23). Show that:
(i) ΔAMC≅ΔBMD
(ii) ∠DBC is a right angle
(iii) ΔDBC≅ΔACB
(iv) CM=12AB

View SolutionIn right triangle ABC , right angle at C, M is the mid-point of the hypotenuse AB. C is jointed to M and produced to a point D such that DM=CM. Point D is joined to point B. Show that AMC≅BMD (ii) ∠DBC=∠ACB DBC≅ACB (iii) CM=12AB
View SolutionABC is a triangle right angled at C and M is mid-point of hypotenuse AB. Line drawn through M and parallel to BC intersects AC at D. Show that:
MD is mid-point of AC.
View SolutionIf D is the mid-point of the hypotenuse AC of a right triangle ABC, prove that BD=12AC
View SolutionIn a right ABC right-angled at C , if D is the mid-point of BC , prove that BC2=4 (AD2−AC2) .
View SolutionIn the adjoining figure, ΔABC is right angled at C and M is the mid-point of hypotenuse AB, If AC = 32 cm and BC = 60 cm, then find the length of CM.

View Solution