In the given figure, PS=PR,∠TPS=∠QPR. Prove that PT=PQ.
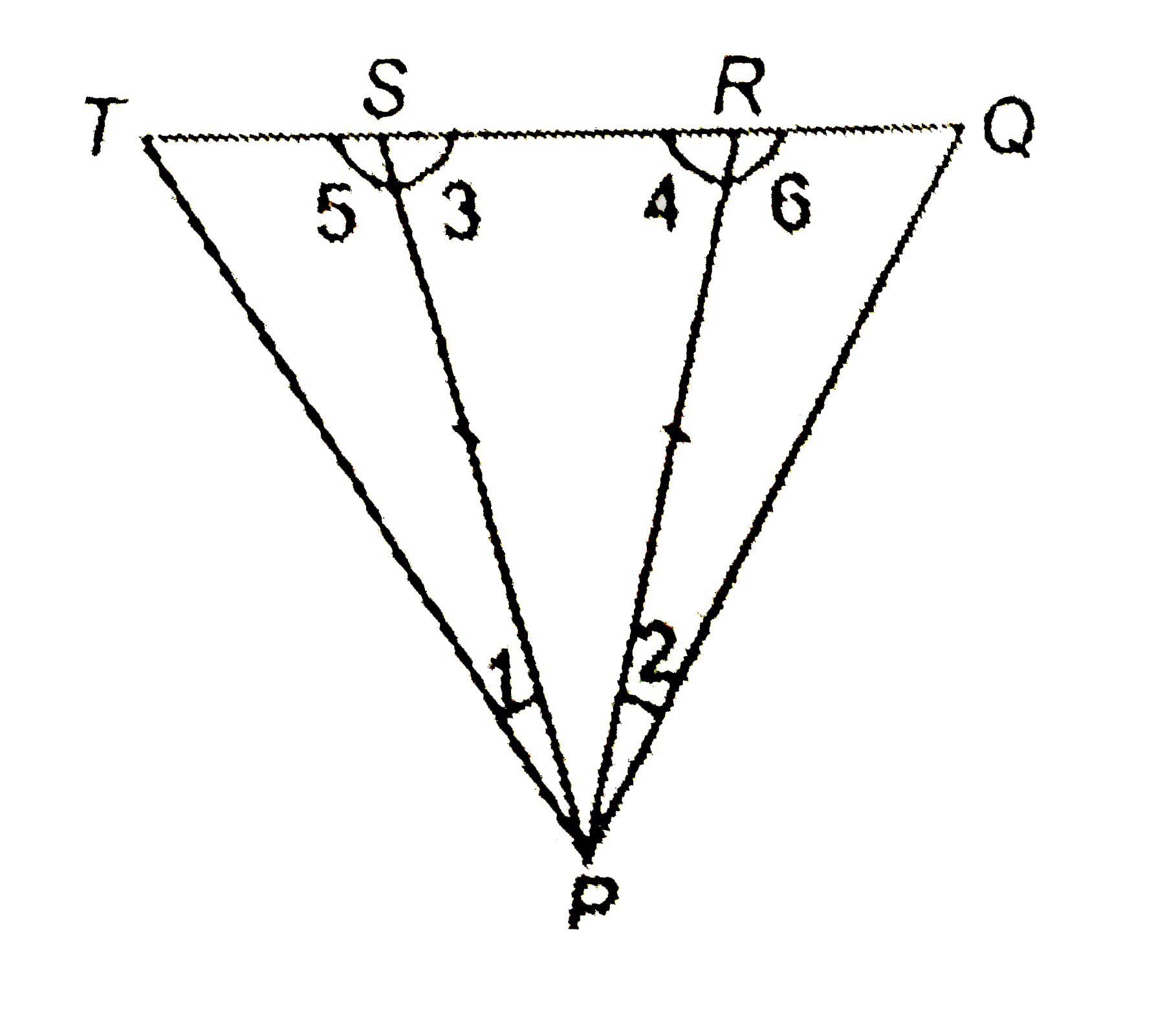
Since PS=PR (given)
∴∠4=∠3 (angle opposite to equal sides are equal)
⇒ 180−∠6=180−∠5 (L.P.A.)
⇒ ∠6=∠5
Now, in ΔPST and ΔPRQ,
∵⎧⎪⎨⎪⎩∠5=∠6(just proved)PS=PR(given)∠1=∠2(given)
∴ΔPST≅ΔPRQ (ASA)
∴PT=PQ (c.p.c.t) Hence Proved.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Problems From NCERT/exemplar5videos
TRIANGLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Exercise 7a35videos
TRIANGLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)10videos
SURFACE AREA AND VOLUME
Similar Questions
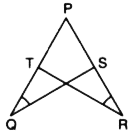
In the given figure, ∠SPR=∠QRP and ∠RSP=∠PQR. Prove that :
(i) PQ=RS
(ii) PS=QR
View SolutionThe given figure shows PQ=PRand∠Q=∠R.
Prove that ΔPQS=ΔPRT
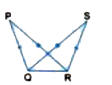
View SolutionIn the given figure, we have PQ=SR and PR=SQ. Prove that :
(i) ΔPQR≅ΔSRQ
(ii) ∠PQR=∠SRQ
View SolutionIn the given figure, ∠PQR=∠PST=90∘, PQ = 5cm and PS = 2 cm.
(i) Prove that ΔPQR~ΔPST.
View SolutionIn the given figure, ∠PQR=∠PST=90∘, PQ = 5cm and PS = 2 cm.
Prove that △PQR ~△PST
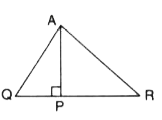
View SolutionIn the given figure , PR>PQ
Prove that : AR>AQ
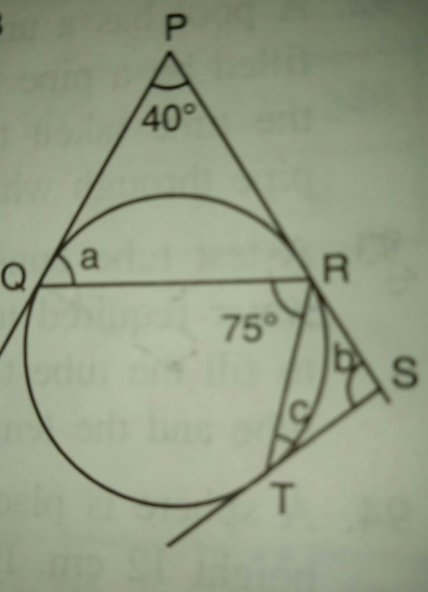
View SolutionIn the given figure, PQ, PR and ST are tangents to the same circle. If ∠P=40∘and∠QRT=75∘, find a, b and c
<
View SolutionIn quadrilateral PQRS , PS = QR and ∠SPQ=∠RQP . Prove that :
PR=QSView SolutionIn the given figure, ∠PQR=∠PST=90∘,PQ=5cmandPS=2cm.
(i) Prove that ΔPQR~ΔPST.
(ii) Find area of ΔPQR : Area of quadrilaterial SRQT.View SolutionIn the given figure if PQ||YZ. Find XQ.
View Solution