Find the deviation using median of the following observations:
15,19,20,28,16.
To find the deviation using the median of the observations 15, 19, 20, 28, and 16, we will follow these steps:
Step 1: Arrange the data in ascending order
First, we need to arrange the given observations in ascending order.
Observations: 15, 19, 20, 28, 16
Arranged Observations: 15, 16, 19, 20, 28
Step 2: Find the median
Next, we will find the median of the arranged data. Since we have 5 observations (which is an odd number), the median is the middle value.
To find the median:
- Total number of observations, n=5
- Median position = n+12=5+12=3
The third observation in the ordered list is 19.
Median = 19
Step 3: Calculate the deviations from the median
Now, we will calculate the deviations of each observation from the median and take the absolute values.
Deviations:
- For 15: |15−19|=|−4|=4
- For 16: |16−19|=|−3|=3
- For 19: |19−19|=|0|=0
- For 20: |20−19|=|1|=1
- For 28: |28−19|=|9|=9
List of Deviations: 4, 3, 0, 1, 9
Step 4: Sum the absolute deviations
Next, we will sum all the absolute deviations calculated in the previous step.
Sum of Deviations:
4+3+0+1+9=17
Step 5: Calculate the mean deviation
Finally, we will calculate the mean deviation using the formula:
Mean Deviation=Sum of Absolute Deviationsn
Where n is the total number of observations.
Mean Deviation=175=3.4
Final Answer
The mean deviation about the median for the given observations is 3.4.
---
First, we need to arrange the given observations in ascending order.
Next, we will find the median of the arranged data. Since we have 5 observations (which is an odd number), the median is the middle value.
- Total number of observations, n=5
- Median position = n+12=5+12=3
Now, we will calculate the deviations of each observation from the median and take the absolute values.
- For 15: |15−19|=|−4|=4
- For 16: |16−19|=|−3|=3
- For 19: |19−19|=|0|=0
- For 20: |20−19|=|1|=1
- For 28: |28−19|=|9|=9
Next, we will sum all the absolute deviations calculated in the previous step.
4+3+0+1+9=17
Finally, we will calculate the mean deviation using the formula:
The mean deviation about the median for the given observations is 3.4.
Topper's Solved these Questions
- STATISTICSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - EXERCISE
20 Videos
- STATISTICSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - NCERT QUESTIONS
27 Videos
- SETSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SETSEXERCISE - MISC Exercise
16 Videos
- STRAIGHT LINESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Exercise
207 Videos
Similar Questions
Find the mean deviation using median for the following observations:
(a) 17,25,9,12,18,26,21
(b) 6,10,11,15,9,7,15,16,5
View SolutionFind the mean deviation using median for the following datas:

View SolutionFind the mean deviation using median:
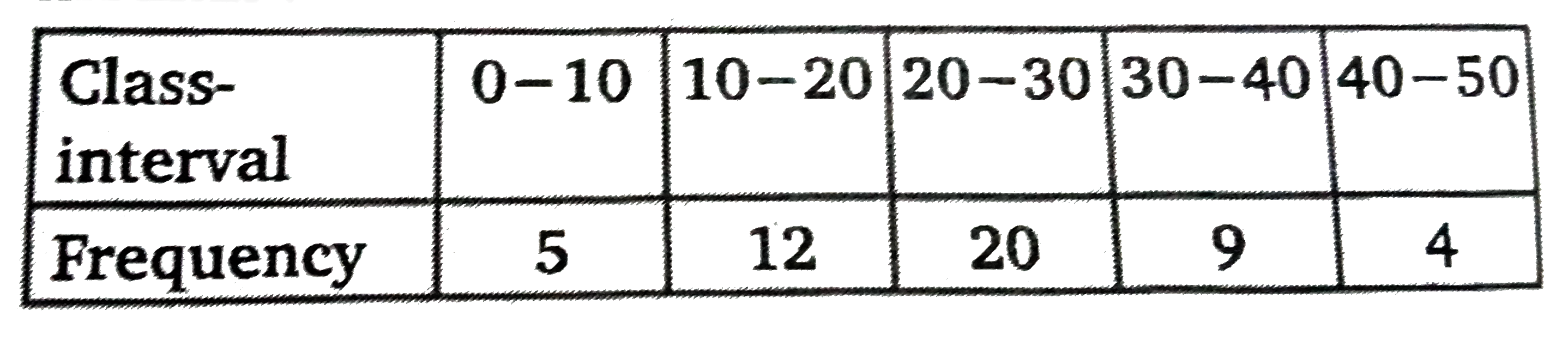
View SolutionFind the mean deviation about median for the following data:

View SolutionFind the mean deviation using arithmetic mean for the following observations:
(a) 68,32,49,54,21,38,59,41,66,76
(b) 28,12,17,35,22,18,5,32
View SolutionFind the mean deviation using arithmetic mean from the folloiwng observations:
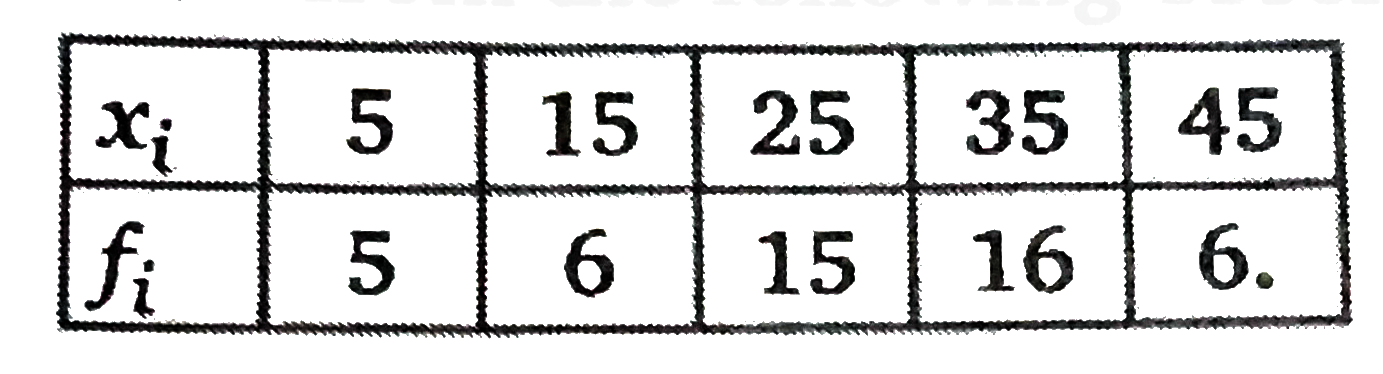
View SolutionCalculate the mean deviation about the median of the following observation: 3011,2780,3020,2354,3541,4150,5000
View SolutionFind the standard deviation from the following observations:
15,18,13,20,17,10,16,19,22,20.
View SolutionFind the mean deviation using arithmetic mean of the following data:
16,22,26,14,12,15,13,18,
View SolutionCalculate the mean deviation about the median of the following observation:22,24,30,27,29,31,25,28,41,42
View Solution
