ABCD is a rectangle with AB=16 units and BC=12 units. F is a point on AB and E is a point on CD such that AFCE is a rhombus. Find the length of EF.
To solve the problem step by step, we will follow these instructions:
Step 1: Understand the Geometry
We have a rectangle ABCD with dimensions AB = 16 units and BC = 12 units. Points F and E are on sides AB and CD respectively, forming a rhombus AFCE.
Step 2: Draw the Rectangle
Draw rectangle ABCD:
- Label the vertices: A (0, 0), B (16, 0), C (16, 12), D (0, 12).
- Identify points F on AB and E on CD.
Step 3: Define Variables
Let AF = x units. Therefore, FB = 16 - x units. Since AFCE is a rhombus, all sides are equal:
- AF = FC = CE = AE = x units.
Step 4: Use the Pythagorean Theorem
In triangle BCF, we have:
- BC = 12 units (vertical side)
- BF = x units (horizontal side)
- CF is the hypotenuse.
Using the Pythagorean theorem:
CF2=BC2+BF2
CF2=122+x2
CF2=144+x2
Step 5: Relate CF to x
Since CF is also equal to the side of the rhombus:
CF=16−x
Thus, we can write:
(16−x)2=144+x2
Step 6: Expand and Simplify
Expanding the left side:
256−32x+x2=144+x2
Now, cancel x2 from both sides:
256−32x=144
Step 7: Solve for x
Rearranging gives:
256−144=32x
112=32x
x=11232=72 units
Step 8: Calculate the Length of the Side of the Rhombus
The length of each side of the rhombus is:
AE=16−x=16−72=322−72=252 units
Step 9: Find the Length of Diagonal AC
Using the Pythagorean theorem in triangle ABC:
AC2=AB2+BC2
AC2=162+122=256+144=400
AC=√400=20 units
Step 10: Calculate Length of EF
Since diagonals of a rhombus bisect each other at right angles, let O be the intersection point of diagonals AC and EF:
- AO = CO = AC2=202=10 units
Using Pythagorean theorem in triangle AOE:
AE2=AO2+OE2
Substituting known values:
(252)2=102+OE2
6254=100+OE2
OE2=6254−100=6254−4004=2254
OE=152=7.5 units
Step 11: Calculate EF
Since EF is twice OE:
EF=2×OE=2×7.5=15 units
Final Answer
The length of EF is 15 units.
---
We have a rectangle ABCD with dimensions AB = 16 units and BC = 12 units. Points F and E are on sides AB and CD respectively, forming a rhombus AFCE.
Draw rectangle ABCD:
- Label the vertices: A (0, 0), B (16, 0), C (16, 12), D (0, 12).
- Identify points F on AB and E on CD.
Let AF = x units. Therefore, FB = 16 - x units. Since AFCE is a rhombus, all sides are equal:
- AF = FC = CE = AE = x units.
In triangle BCF, we have:
- BC = 12 units (vertical side)
- BF = x units (horizontal side)
- CF is the hypotenuse.
CF2=BC2+BF2
CF2=122+x2
CF2=144+x2
Since CF is also equal to the side of the rhombus:
CF=16−x
Thus, we can write:
(16−x)2=144+x2
Expanding the left side:
256−32x+x2=144+x2
Now, cancel x2 from both sides:
256−32x=144
Rearranging gives:
256−144=32x
112=32x
x=11232=72 units
The length of each side of the rhombus is:
AE=16−x=16−72=322−72=252 units
Using the Pythagorean theorem in triangle ABC:
AC2=AB2+BC2
AC2=162+122=256+144=400
AC=√400=20 units
Since diagonals of a rhombus bisect each other at right angles, let O be the intersection point of diagonals AC and EF:
- AO = CO = AC2=202=10 units
AE2=AO2+OE2
Substituting known values:
(252)2=102+OE2
6254=100+OE2
OE2=6254−100=6254−4004=2254
OE=152=7.5 units
Since EF is twice OE:
EF=2×OE=2×7.5=15 units
The length of EF is 15 units.
Topper's Solved these Questions
- HERONS'S FORMULABOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - HERONS'S FORMULAEXERCISE - Problems From NCERT / Exemplar
10 Videos
- HERONS'S FORMULABOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - HERONS'S FORMULAEXERCISE - Exercise 12a
11 Videos
- CONSTRUCTIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - EXERCISE
36 Videos
- INTRODUCTION TO EUCLID'S GEOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - INTRODUCTION TO EUCLID'S GEOMETRYEXERCISE - Exercise
8 Videos
Similar Questions
Let ABCD be a rectangle such that AB=10 units and BC=8 units. Taking AB and AD as x and y axis respectively, find the coordinates of A, B, C and D.
View SolutionIn triangle ABC, angle B is obtuse. D and E are mid-points of sides AB and BC respectively and F is a point on side AC such that EF is parallel to AB. Show that BEFD is a parallelogram.
View Solution
Knowledge Check
In the figure, ABCD is a rectangle. Points E and F cut the sides BC and CD of the rectangle respectively such that EC = 3, FC = 4, and AD = 12, and the area of the crossed and the shaded regions in the figure are equal. Which one of the following equals the perimeter of rectangle ABCD?
 A42B50C56D64
A42B50C56D64In the figure, ABCD is a rectangle, and F and E are points on AB and BC respectively. The area of ΔDFB is 9 and the area of ΔBED is 24. What is the perimeter of the rectangle?
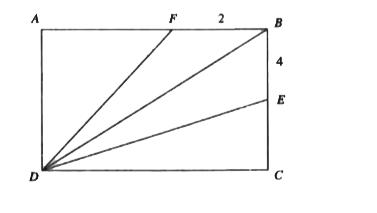 A18B23C30D42
A18B23C30D42In the figure below, ABCD is a rectangle, EFGH is a square, and ¯¯¯¯¯¯CD is a diameter of a semicircle. Point K is the midpoint of ¯¯¯¯¯¯CD. Point J is the midpoint of both ¯¯¯¯¯¯AB and ¯¯¯¯¯¯EF. Points E and F lie on ¯¯¯¯¯¯AB. The 3 given lengths are in meters.
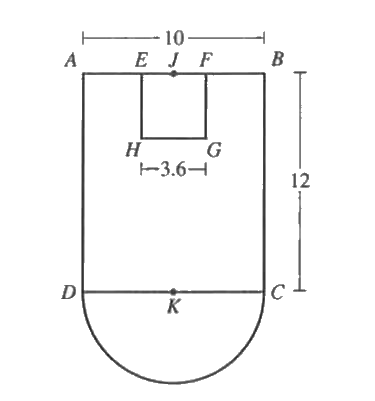
What is the length, in meters, of are ¯¯¯¯¯¯CD?A2.5πB5πC6.25πD10π
If ABC is a triangle such that A=(1,2)andB=(5,5) with BC=9andAC=12 units, if slope of altitude CD is (D is point on AB) is m/n, then minimum vlaue of m2+n is _______
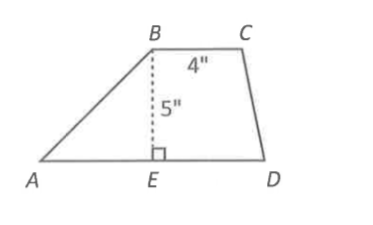
View SolutionABCD is a quadrillateral, with AD parallel to BC (see figure). E is a point between A and D such that BE represents the height of ABCD and E is the midpoint of AD. If the area of triangle ABE is 12.5 square inches, what is the area of ABCD?
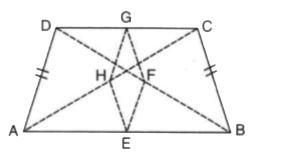
View SolutionABCD is a quadrilateral in which AD = BC. E, F, G and H are the mid-points of AB, BD, CD and AC respectively. Prove that EFGH is a rhombus.
View SolutionABCD is a trapezium with AB || DC. E and F are points on non-parallel sides AD and BC respectively such that EF is parallel to AB. Show thatAEED=BFFC.
View SolutionABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that

BC= BE
View Solution
