Question

The figure formed by
joining the mid-points of the adjacent sides of a rectangle is
square (b) rhombus
(c) trapezium (d)
none of these

Explanation

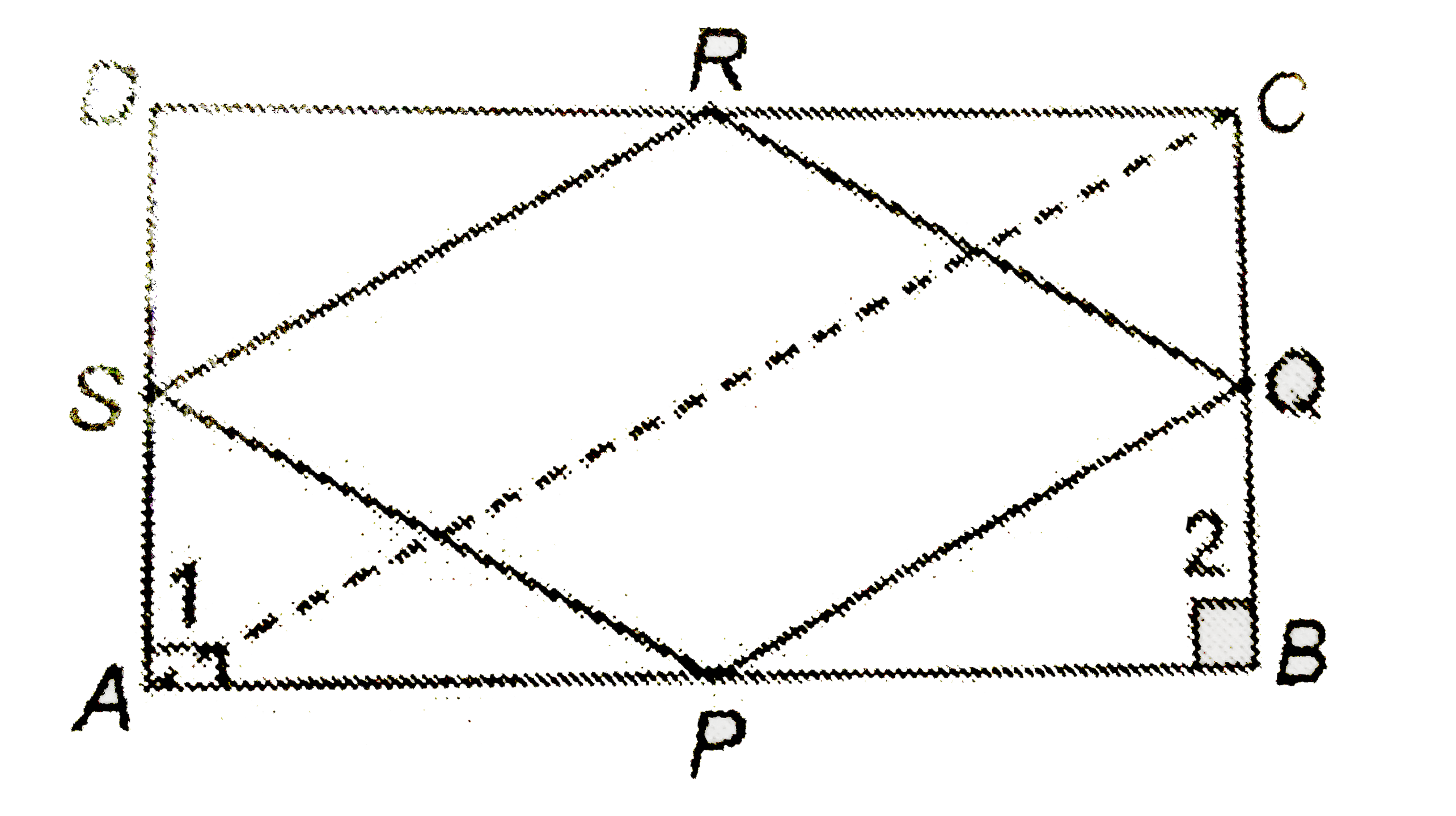
Given : `square ABCD` is a rectangle in which P,Q, R and S are the mid-point of AB, BC, CD and DA respectively.
To prove : `square PQRS` is a rhombus.
Construction : Join AC.
Proof. First of all we will prove,`square PQRS` is a parallelogram . Then two consecutive sides of a parallelogram are equal i.e., PS=PQ. In this way we can get a rhombus.
In `triangle`, since P and Q ar the mid-points of AB and BC respectively.
`therefore PQ"||"AC and PQ=(1)/(2)AC" "` ("mid-point theorem")...(1)
Now ,in `triangleADC,` sicne S and R are the mid-points of AD and DC respectively.
`therefore SR"||"AC and SR=(1)/(2)AC" "(mid-point theorem)...(2)`
`therefore` From (1) adn (2) , we get
`PQ"||"SR and PQ=SR`
Thus, in equilateral PQRS, one pair of opposite sides in parallel sides in parallel and equal .
`therefore square PQRS` is a parallelogram.`" " ...(3)`
Since, `AD=BC" " `(opposite sides of a rectangle)
`implies (1)/(2)AD =(1)/(2)BC`
`implies SA=QB" "`(`because` S and Q are the mid-points)
Thus, in `triangleSAP, and triangleQBP`
`therefore {{:(SA=QB" "("just proved")),(angle1=angle2" "("each " 90^(@) "as angle of rectangle")),(AP=BP" "(therefore "P is the mid -point of AB")):}`
`therefore " "triangleSAP~=triangleQBP, " "` (SAS criterion of congruence)
`implies PS=PQ" "`(c.p.c.t)...(4)