ABCD is a parallelogram. Two points P and Q are taken on sides AD and BC respectively such that AP Prove that is a parallelogram.
To prove that quadrilateral AQCP is a parallelogram, we need to show that one pair of opposite sides is both equal and parallel. Let's follow the steps systematically.
Step 1: Identify the points on the parallelogram
Given that ABCD is a parallelogram, we have:
- Points P and Q are located on sides AD and BC respectively.
- It is given that AP=13AD and CQ=13BC.
Step 2: Establish the relationships between the sides
Since ABCD is a parallelogram, we know:
- AD∥BC and AD=BC (opposite sides of a parallelogram are equal and parallel).
Step 3: Determine the lengths of segments
From the given information:
- Since AP=13AD, we can express PD as:
PD=AD−AP=AD−13AD=23AD
- Similarly, since CQ=13BC, we can express BQ as:
BQ=BC−CQ=BC−13BC=23BC
Step 4: Show that segments AP and CQ are parallel
Since AD∥BC, it follows that:
- AP∥CQ because they are both segments taken from lines that are parallel.
Step 5: Show that segments AP and CQ are equal
Since AD=BC, we can substitute:
- AP=13AD and CQ=13BC.
Thus, we have:
AP=CQ
This shows that AP is equal to CQ.
Step 6: Conclude that AQCP is a parallelogram
Now we have established that:
- AP∥CQ (both are parallel)
- AP=CQ (both are equal)
According to the properties of a parallelogram, if one pair of opposite sides is both equal and parallel, then the quadrilateral AQCP is a parallelogram.
Final Statement
Thus, we have proved that quadrilateral AQCP is a parallelogram.
---
Given that ABCD is a parallelogram, we have:
- Points P and Q are located on sides AD and BC respectively.
- It is given that AP=13AD and CQ=13BC.
Since ABCD is a parallelogram, we know:
- AD∥BC and AD=BC (opposite sides of a parallelogram are equal and parallel).
From the given information:
- Since AP=13AD, we can express PD as:
PD=AD−AP=AD−13AD=23AD
- Similarly, since CQ=13BC, we can express BQ as:
BQ=BC−CQ=BC−13BC=23BC
Since AD∥BC, it follows that:
- AP∥CQ because they are both segments taken from lines that are parallel.
Since AD=BC, we can substitute:
- AP=13AD and CQ=13BC.
Thus, we have:
AP=CQ
This shows that AP is equal to CQ.
Now we have established that:
- AP∥CQ (both are parallel)
- AP=CQ (both are equal)
Thus, we have proved that quadrilateral AQCP is a parallelogram.
Topper's Solved these Questions
- QUADRILATERALSBook:NAGEEN PRAKASHAN ENGLISHChapter:QUADRILATERALSExercise:Problems From NCERT/exemplar
Explore 11 Videos
- QUADRILATERALSBook:NAGEEN PRAKASHAN ENGLISHChapter:QUADRILATERALSExercise:Exercise 8a
Explore 29 Videos
- PROBABILITYBook:NAGEEN PRAKASHAN ENGLISHChapter:PROBABILITYExercise:Revision Exercise (very Short Answer /short Answer Questions)
Explore 10 Videos
- STATISTICSBook:NAGEEN PRAKASHAN ENGLISHChapter:STATISTICSExercise:Revision Exercise
Explore 12 Videos
Similar Questions
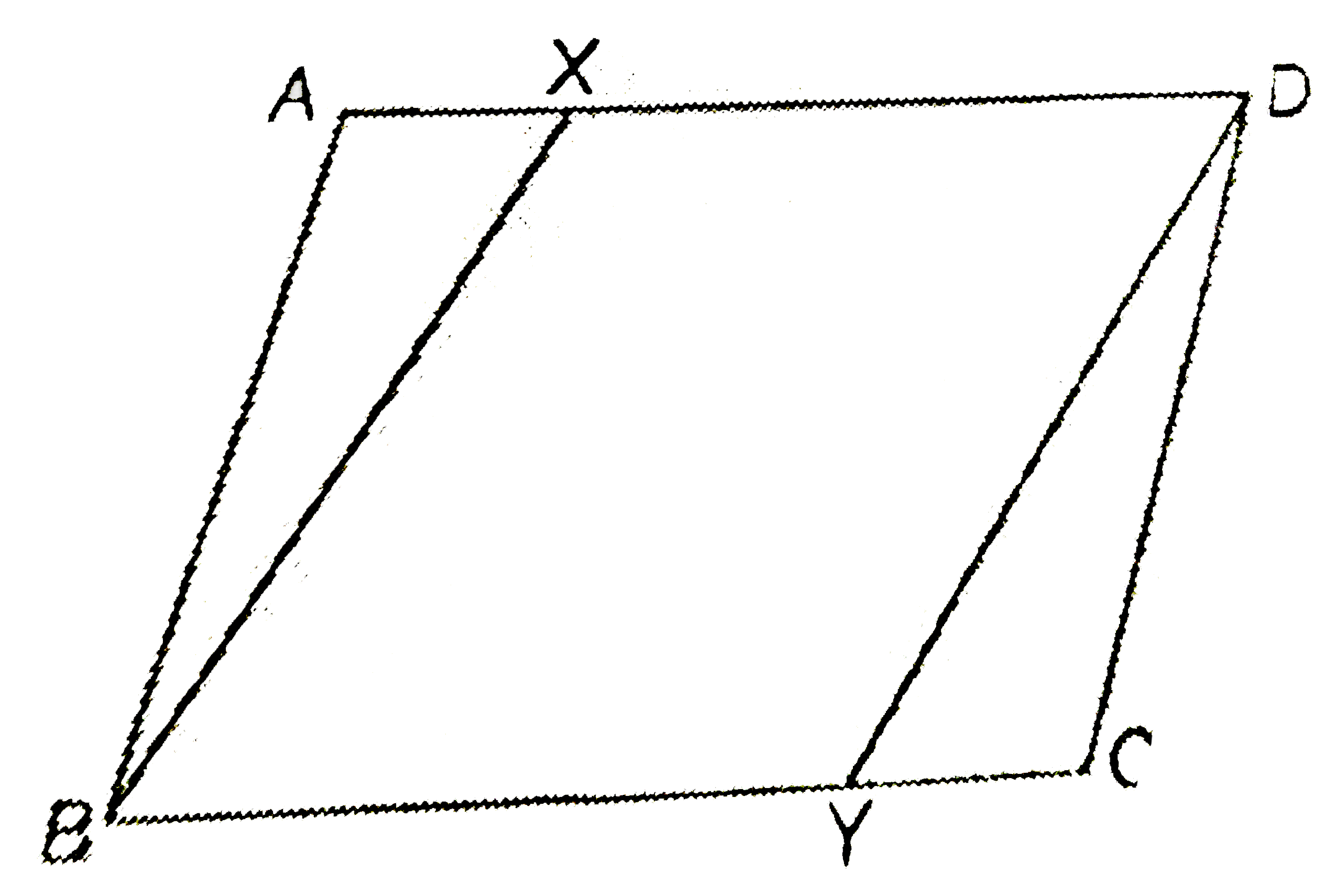
In the adjoining figure □ABCD is a parallelogeam. Points X and Y lie on the sides AD and BC respectively and AX=14ADandCY=14BC. Show that □XBYD is a parallelogram.
View SolutionABCD is a square, X and Y are points on sides AD and BC respectively such that AY=BX. Prove that BY=AX and ∠BAY=∠ABX.
View SolutionABCD is a parallelogram. The sides AB and AD are produced to E and F respectively, such that AB = BE and AD = DF. Prove that : ΔBEC≅ΔDCF.
View SolutionABCD is a parallelogram. P is a point on AD such that AP=13 AD and Q is a point on BC such that CQ=13BC. Prove that AQCP is a parallelogram.
View SolutionABCD is a parallelogram. P and Q are the mid-points of sides AB and AD reapectively.
Prove that area of triangle APQ= 18 of the area of parallelogram ABCD.
View SolutionABCD is a parallelogram. P and Q are the mid-points of sides AB and AD reapectively.
Prove that area of triangle APQ= 18 of the area of parallelogram ABCD.
View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of triangle ABC. Prove that:
BDEF is a parallelogram.
View SolutionABCD is a square. P, Q and Rare the points on AB, BC and CD respectively, such that AP = BQ = CR. Prove that:
PB = QC
View SolutionABCD is a square. P, Q and Rare the points on AB, BC and CD respectively, such that AP = BQ = CR. Prove that:
PQ = QR
View SolutionP,Q,R are the points on the sides AB, BC and CA respectively of triangle ABC such that AP:PB=BQ:QC=AR:RC=1:2. Show that PBQR is a parallelogram.
View Solution
