In the given figure, ABCD is a parallelogram in which AN and CP are perpendiculars on diagonal BD. Prove that :
(i) ΔADN=ΔCBP
(ii)AN=CP
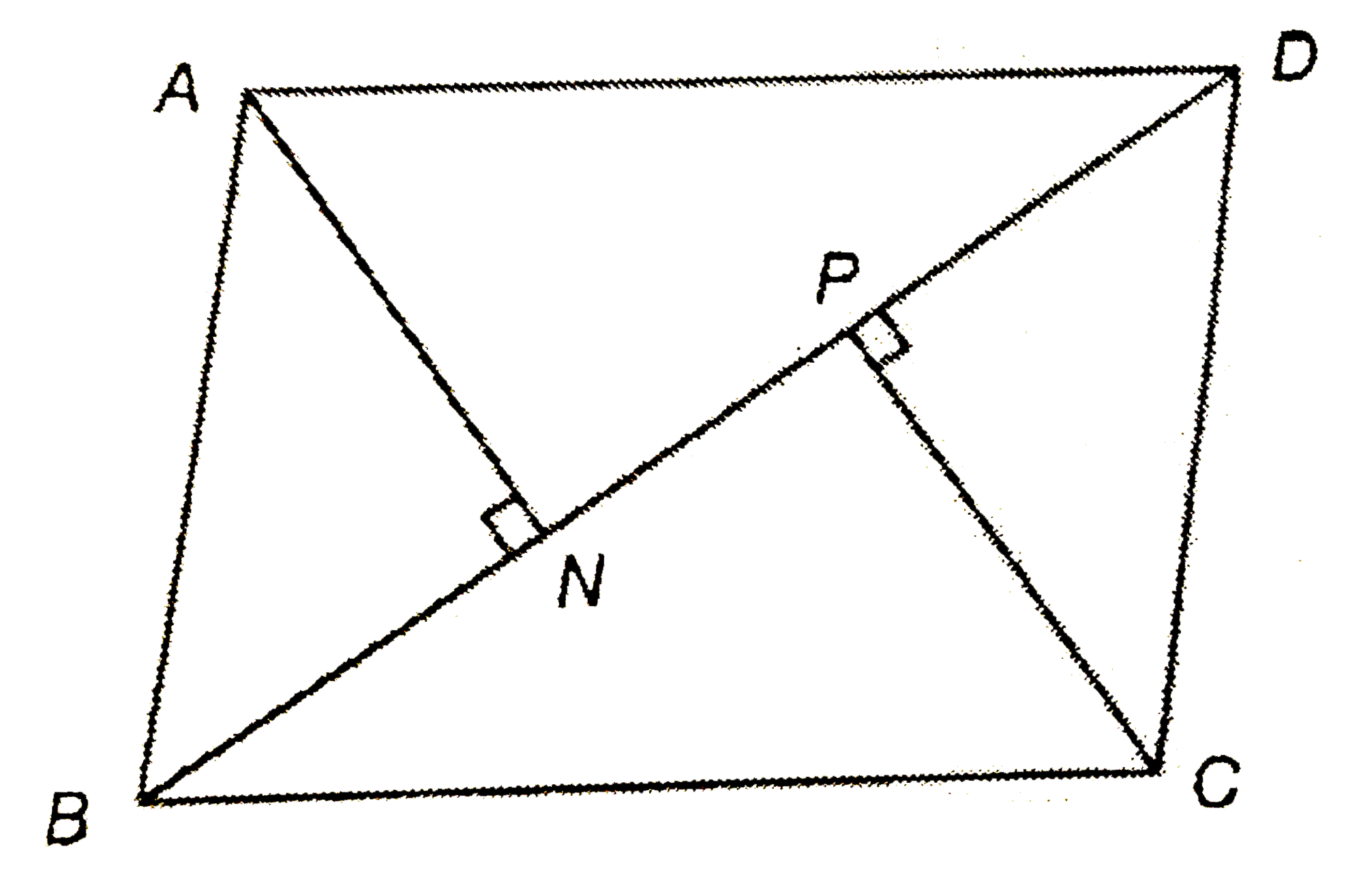
(i)InΔADNandΔCBP
∵⎧⎪⎨⎪⎩∠AND=∠CBP(each90∘)AD=CB(opposite sides of a parallelogram)∠ADN=∠CVBP(alternate anglesAD∣∣BC
∴ ΔADH≅ΔCBP (AAS theorem)
(ii)∵ ΔADN≅ΔCBP
∴ AN∣CP (c.p.c.t)
Topper's Solved these Questions
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Problems From NCERT/exemplar
11 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Exercise 8a
29 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- STATISTICSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - Revision Exercise
12 Videos
Similar Questions
Knowledge Check
In the figure, ABCD is a parallelogram. Which one of the following is true?
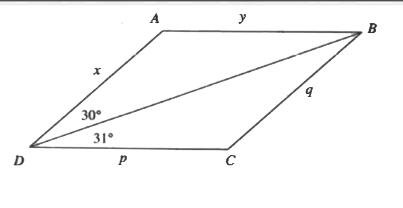 Ax<yBx>qCx>pDy>p
Ax<yBx>qCx>pDy>p
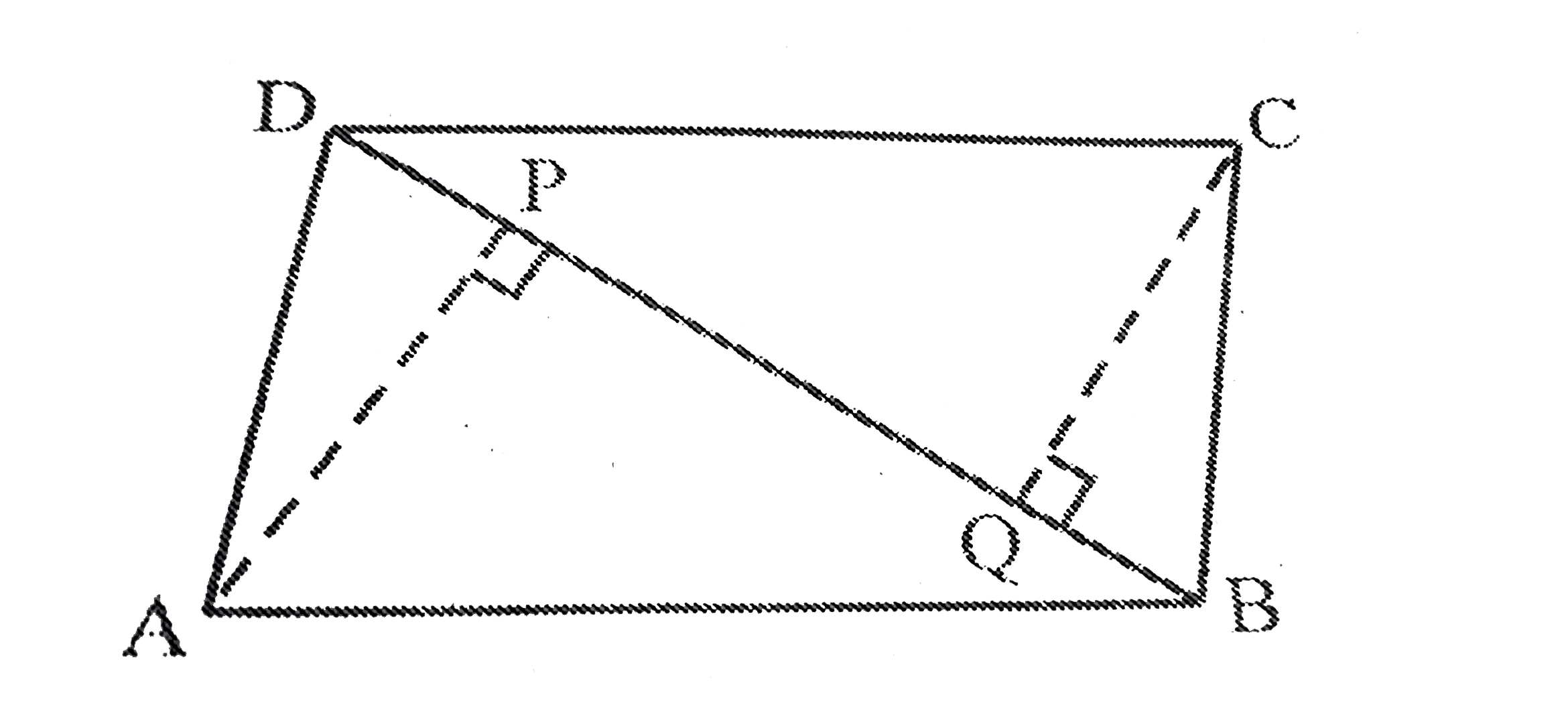
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD . Show that
(i) ΔAPB≅ ΔCQD
(ii) AP = CQ
View SolutionIn the following figure, ABCD is a parallelogram. Prove that:

BP bisects angle B
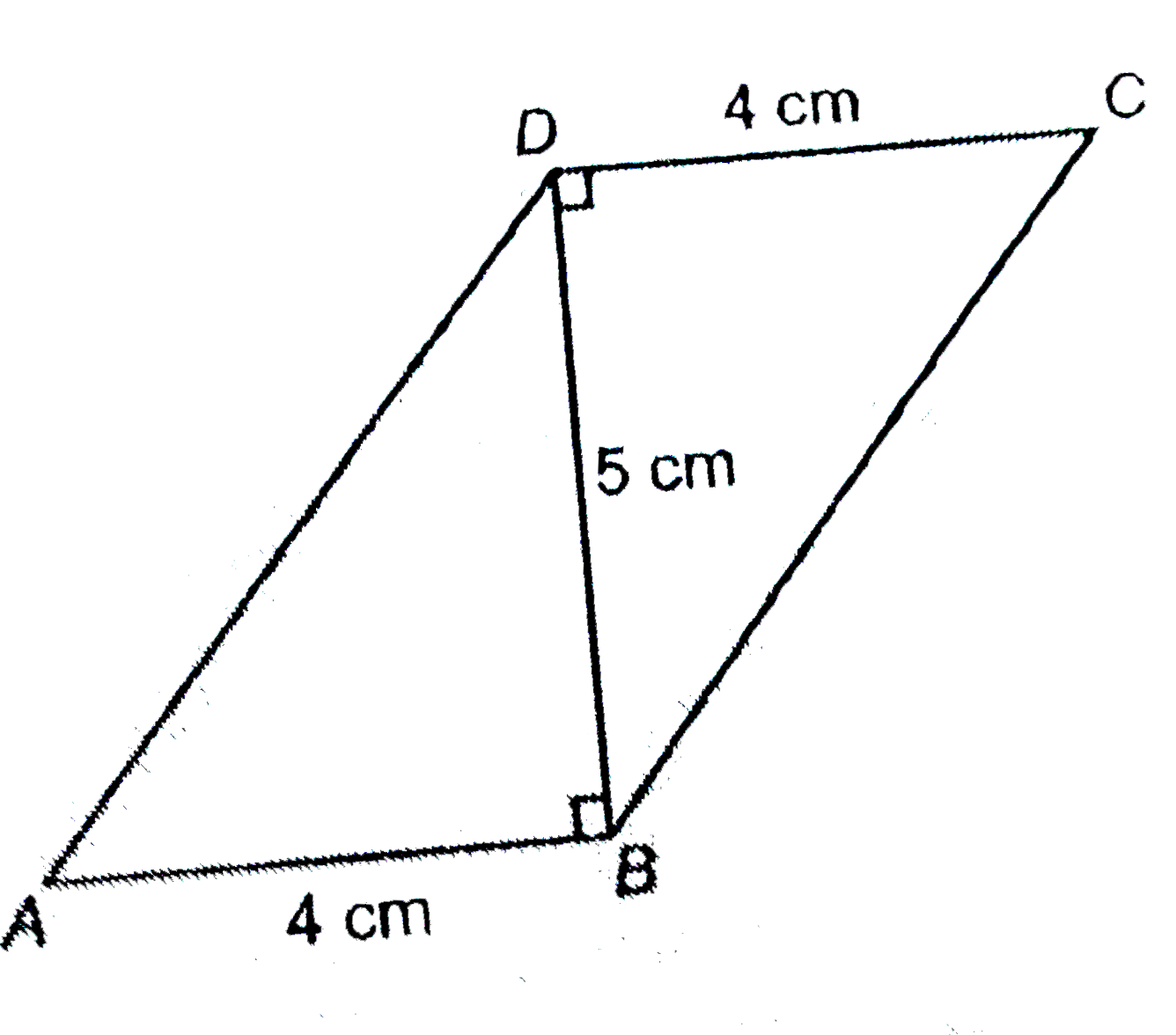
View SolutionIn the adjoining figure, prove that ABCD is a parallelogram. Also find its area.
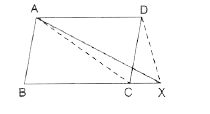
View SolutionIn the given figure, ABCD is a parallelogram BC is produced to point X. prove that :
area(ΔABX)=area( .ACXD)
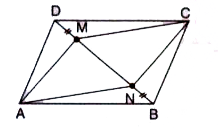
View SolutionThe given figure shows parallelogram ABCD. Points M and N lie in diagonal BD such that DM=BN
 .
.
Prove that:
(i) ΔDMC≅ΔBNA and so CM=AN.
(ii) ΔAMD≅ΔCNB and so AM=CN.
(iii) ANCM is a parallelogram.
View SolutionIn the given figure, ABCD is a square. M is the mid-point of AB and PQ is perpendicular to CM. CB produced meets PQ at point Q. Prove that :
(i) PA = BQ
(ii) CP = AB + PA

View SolutionIn Figure, AN and CP are perpendicular to the diagonal BD of a parallelogram ABCD. Prove that :
(i) ADN≅CBP
(ii) AN=CP
View Solution


